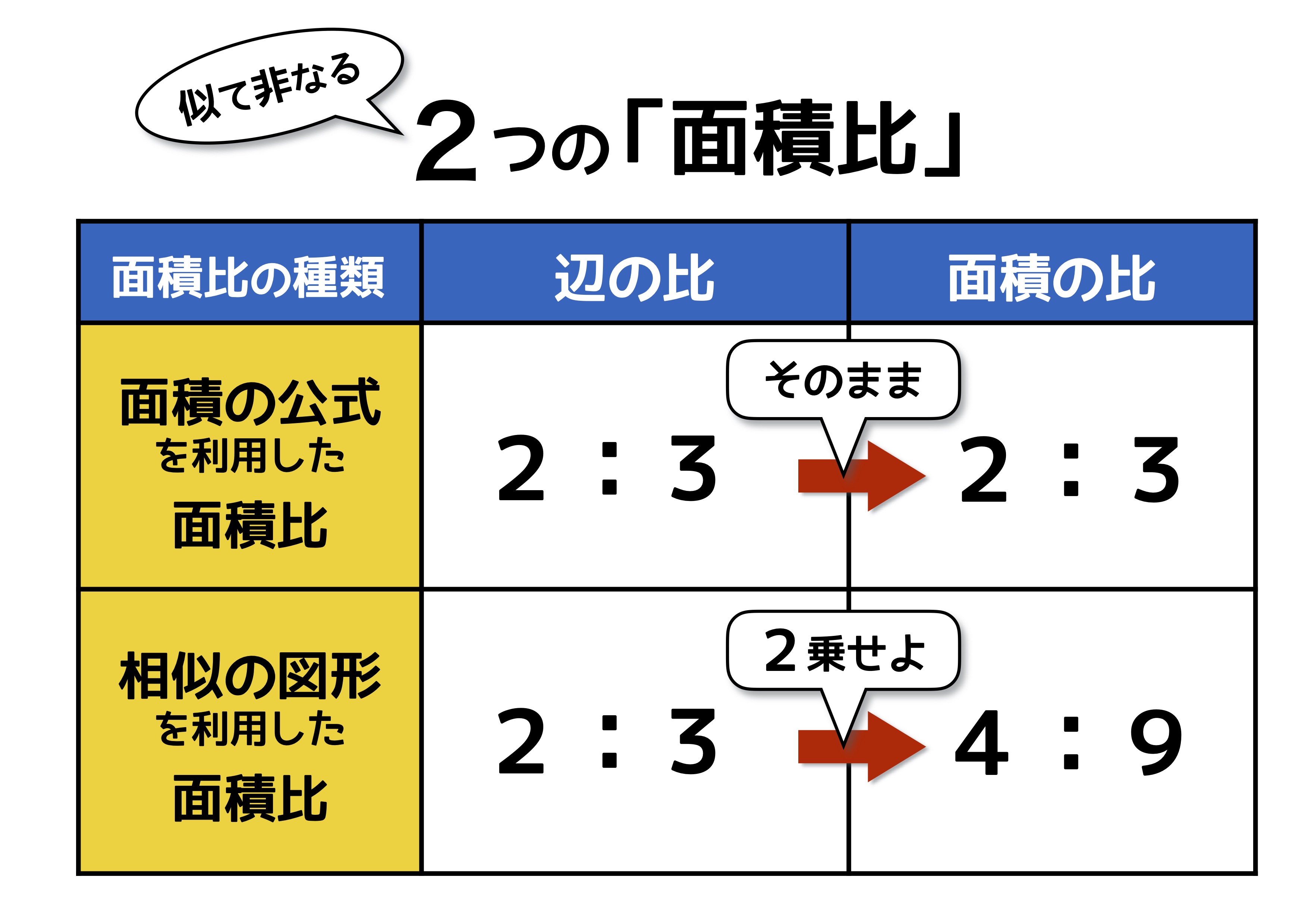
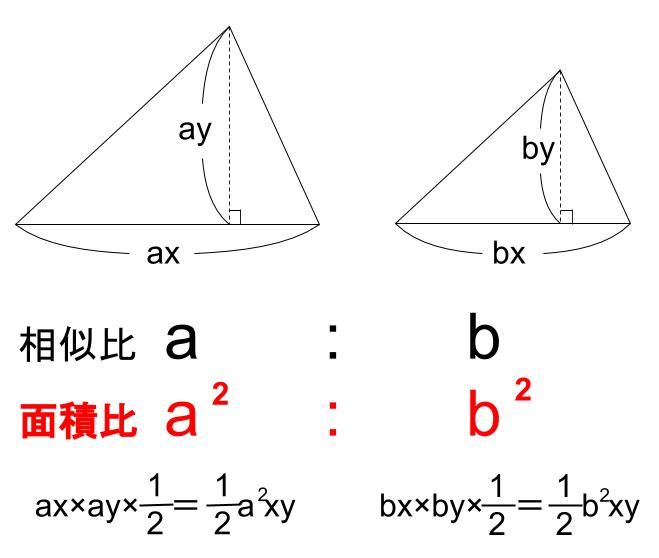
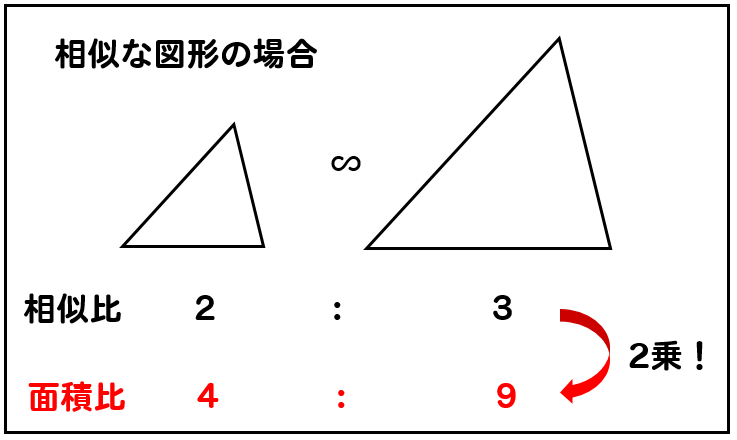
相似比が1:2 なら、 底辺も2倍 になるし、 高さも2倍 になるから、 2 2 で4倍 。 面積比は1:4 になるわけだよ。18/8/21 図形と計量三角形の辺の長さを求めるときの三角比の値 xの値を求めよ。という問題で, これを解こうとすると,sin45°,sin60°という三角比が出てきました。 定義では,「直角三角形」だけで考えるとありました。対象 小学5年~ 予習シリーズ該当回 5年下第13回 内容 平面図形と比の学習 平面図形と比の学習はこちらへ↓ 平面図形と比1 平面図形と比2

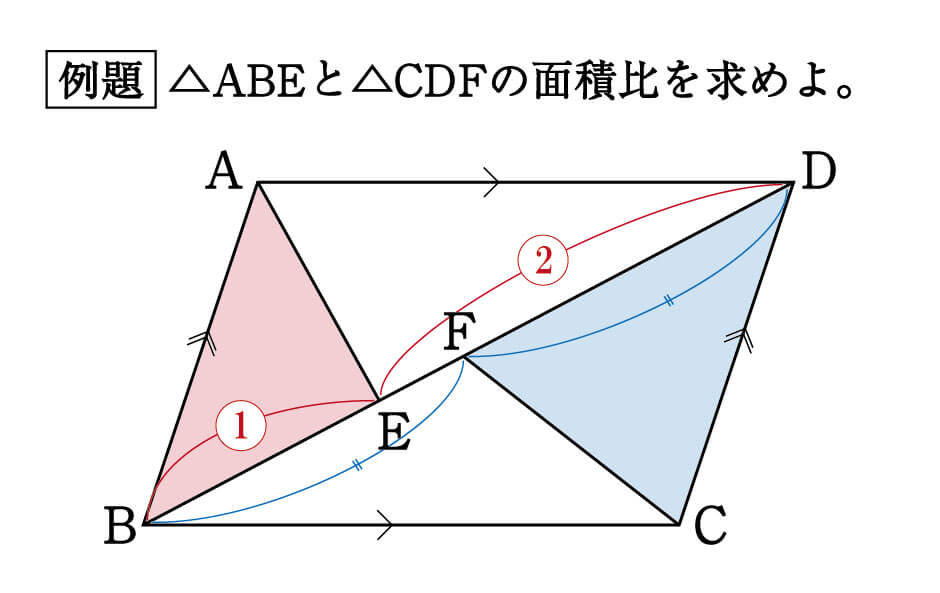
中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ
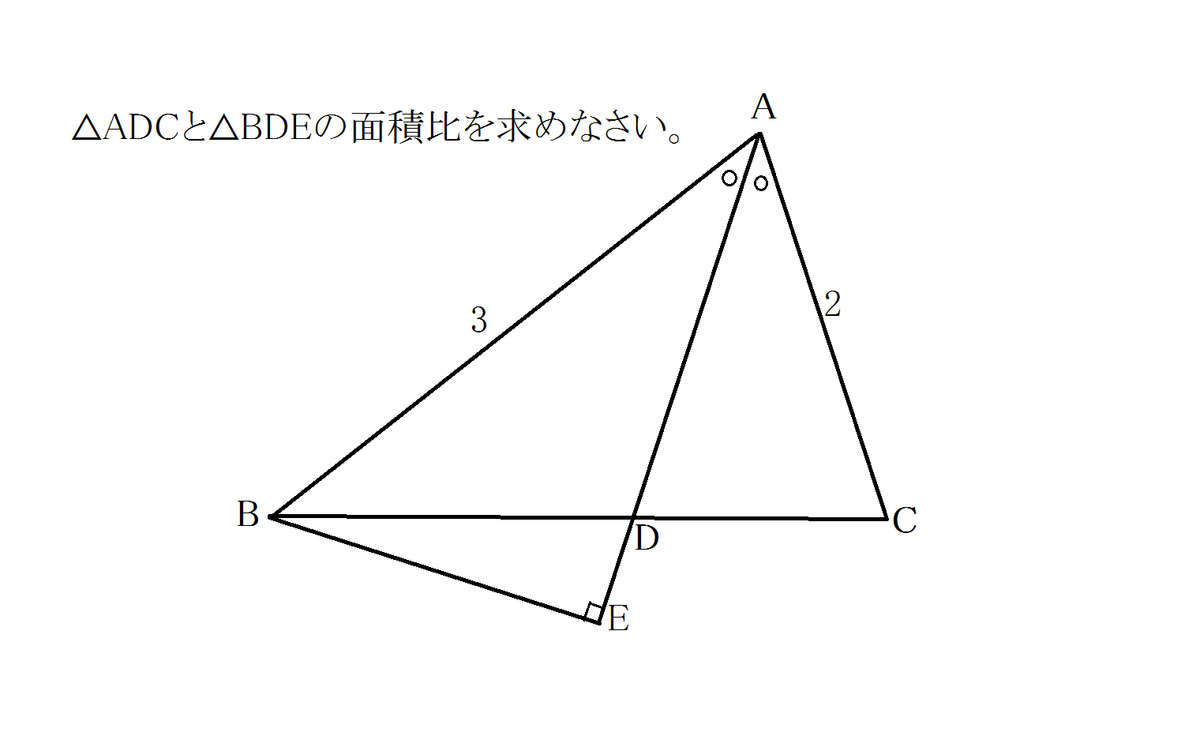
中2 数学 図形 比
中2 数学 図形 比-10/2/18 数学Ⅰ 図形と計量三角比の登場。定義をしっかり確認しましょう。 三角比の導入 数学で使う重要な三角比とその導出 三角比の相互関係とその使い方 定義からわかる三角比の有用性 (補足)三角比の相互関係の導出 三角比の拡張と単位円 \(0^\ci31/5/21 これらを活用し,平面図形や空間図形について,辺の長さ,角度,面積,体積などのさまざまな計算や計量を行います。 2.何ができればよいか ① 30°,45°,60°の三角比がすぐ言えるようにする。 ② 三角比の相互関係の公式を覚える。



相似な図形 面積比の問題 苦手な数学を簡単に
三角比 A 三角比の導入 2Aつの直角三角形において•A直角でない角が等しければ•AそのAつの直角三角形は 相似であるから•A対応する辺の比は等しい. θ=θ'Aのとき, b c = b c' かつ a c = a' c補角をなす三角形の面積比 解説 2つの角∠a,∠bが,∠a∠b=180°となるとき,∠aと∠bは,たがいに補角の関係にあるといいます。 ここで次の図のように,1組の角(∠bcaと∠ecd)がたがいに補角をなす(∠bca∠ecd=180°)三角形( abcと ecd)の面積比を考えます。図形の性質を三角形の相似条件などを基にして確かめ,論理的に考察し表現する能力を伸ばし, 相似な図形の性質を用いて考察することができる。 3 単元の評価規準 数学への 関心・意欲・態度 数学的な見方や考え方 数学的な技能 数量や図形などに
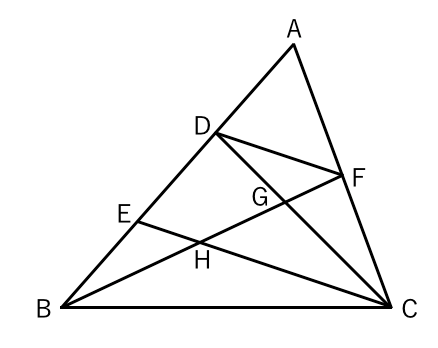
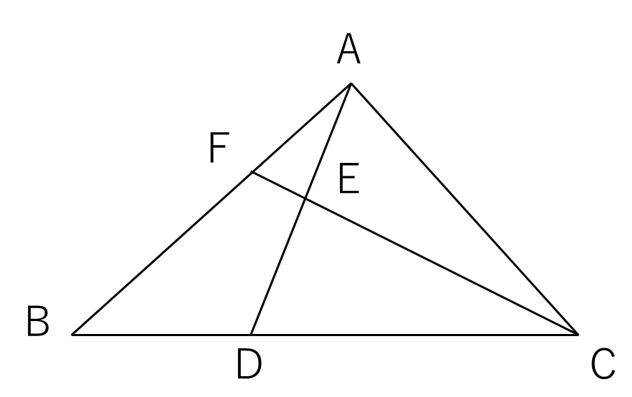
A B C M ADDB=AEEC=11, DFFC=EFFB=12である。 A B C D E F 面積比 DFE DFBを求めよ。 面積比 ADE DBEを求めよ。 面積比 DFE ABCを求めよ。 次の問いに答えよ。 DがBCの中点、EがADの中点のとき面積比 AEC ABCを求めよ。 A B C D E BDDC=43, AEED=23のとき、面積比 EDC ABCを求めよ。 A B C D E14/7/18 数学入試で差がつく、線分比と面積比の関係をサクッとまとめました中学数学 図形 三角形の線分比と面積比の関係について パート2 今回の内容は、具体的には、以下のような、相似な図形の「周長比」は、相似比の「そのもの」に等しい ・ 相似な図形の「面積比」は、相似比の「2乗」に等しい ・ 相似な図形の「表面積比」は、相似比の「2乗」に等しい ・ 相似な図形の「体積比」は、相似比の「3乗」に等しい
相似を表す記号 4ABC と4DEF が そうじ 相似のとき 4ABC ˝ 4DEF と表す. 三角形の相似条件 a b c ka kb kc a b ka kb 三角形が相似になる条件は次である. 1 3 辺の辺の比がすべて等しい ˆ 相似比1 k 2 2 辺の辺の比とその間の角がそれぞれ等しい ˆ 相似比1 kAmazonで坂田アキラの改訂版 坂田アキラの 三角比・平面図形が面白いほどわかる本 (坂田アキラの理系シリーズ)。アマゾンならポイント還元本が多数。坂田アキラ作品ほか、お急ぎ便対象商品は当日お届けも可能。また改訂版 坂田アキラの 三角比・平面図形が面白いほどわかる本 (坂田アキラの1角共有の三角形の面積比 解説 次の図の abcと adeのように,1つの角(∠a)が共有されている2つの三角形の面積比について考えます。




数学 入試で差がつく 線分比と面積比の関係をサクッとまとめました 中学数学 図形 行間 ぎょうのあいだ 先生



相似な図形 平行線と線分の比 よく出る系 苦手な数学を簡単に
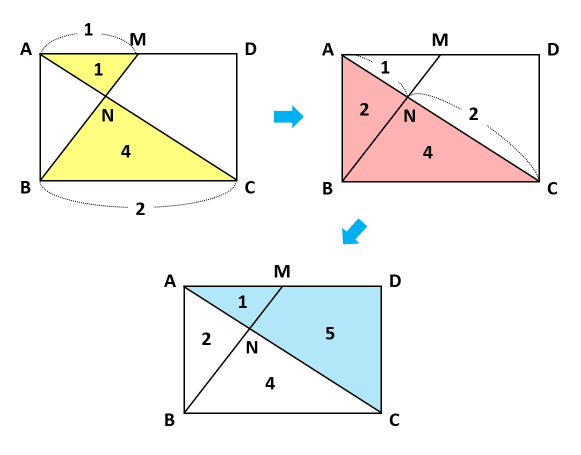
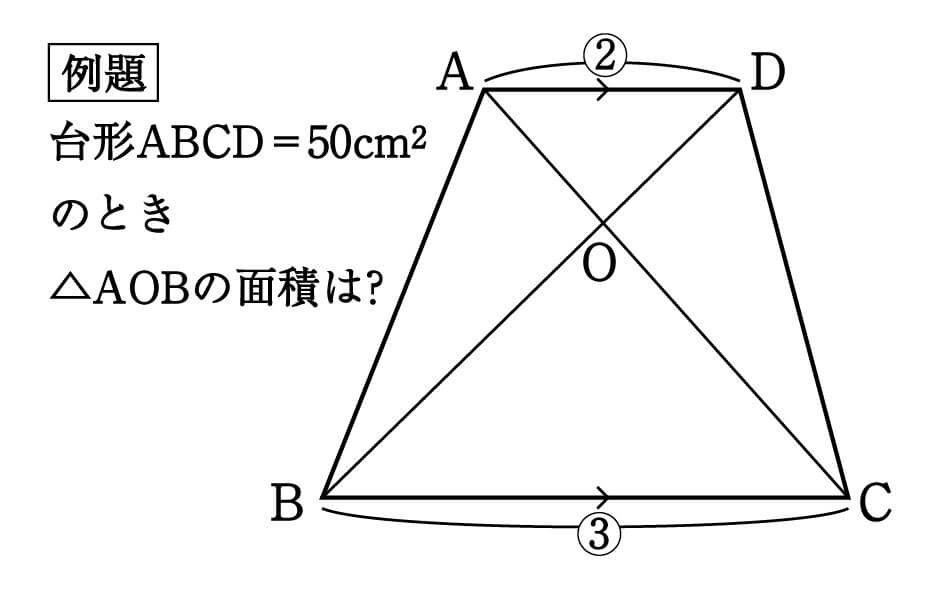
三角形の左側に注目すると、 ABEと BDEは「高さが同じ隣り合う三角形」であることがわかります。 ①の型に該当するので、2つの面積比は底辺比に等しい。 つまり ABE: BDE=2:1となるわけです。 続いて、 ABDと ACDを見てみると、こちらも①の型に当てはまります。 ABDの面積を、 ABEと BDEを合わせて3とした場合、 ABDと ACDの面積比は、底辺の比が3:5なので4/1/21 台形abcdがあり、上底adと下底bcの比は2:3です。 台形の面積が50cm 2 であるとき、 aobの面積はいくつでしょうか? という問題です。 問題文には‟面積比"という言葉が使われていませんが、2つの異なる図形の面積を比べる問題なので、これも面積比のパターンの1つです。数学35章図形と相似「平行線と線分の比」<準備問題> 組 番 名前 1平行四辺形の定義を書きなさい。 2四角形が平行四辺形であるための条件が3つ書いてあります。あと2つ,条件を書きなさい。 ・2組の向かい合う辺がそれぞれ平行である。



中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su




平面図形をマスター 三角形の面積比 応用編その3
数学 相似な図形 平行線と比 釜石市立釜石中学校 平成24年11月 9日 246 jh_su 中 3 数学 相似な図形 滝沢村立滝沢第二中学校 平成24年10月26日 245 jh_su 中 3 数学 相似な図形 紫波町立紫波第三中学校 平成24年10月18日 244 jh_su 中 3 数学 2 相似な図形の面積比の問題です。基本を確認して、いろいろな応用問題を解けるようにしてください。基本事項相似比が m n である図形の面積の比は,m2 n2 である。例)下のような相似な三角形がある ABCと A'B'C'の相似比は 1:2面積を求めると ABC=4 A'B'C'=16 面積比は1:4相似比が1:2のとき空間図形の表面積比と体積比 右の図のように、2つの立体が相似ならば、対応する表面の図形も互いに相似である。 それゆえ、相似比が m n の図形の表面比は S S ′ = m 2 n 2 となる。 また、左の三角推の底面積と高さを T 、 h とすると、右の三角錐の底面積と高さは T × n 2 m 2 、 h × n m となるから V V ′ = 1 3 T h 1 3 × T n 2 m 2 × h n 2 m 2 = 1 n 3 m 3 = m 3 n 3 となる



中3数学 相似や比の応用問題を解くためのテクニック 個別指導塾のyou 学舎日記 公式ブログ



Studydoctor相似比と辺の比 中学3年数学 Studydoctor
相似な図形の場合、 相似比を2乗して面積比を作りましょう! 面積比が分かったら、あとは楽勝だね (^^) 図形Bの面積を とおいて、比例式を作っていきましょう。 よって、図形Bの面積は ㎠ となります。 相似比の2乗だ! ってことを覚えておけば簡単です (^^) 問題 次の図において、 の面積が ㎠ であるとき、 の面積を求めなさい。 と は相似な図形にはなって 図形と相似の最終回です。 計算に関する問題が中心となりますが、 特に面積比・体積比はしっかりと練習しておきましょう。 11.角の二等分線と線分比 eclus13 215K subscribers Subscribe 角の二等分線と線分比 中3数学 図形と相似11中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード・印刷;




中学数学 相似比の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ
香川亮の数学基本大全 三角比 数学i61a 空間図形と三角比 三角比数学Ⅰ 図形と計量 数学A 図形の性質 第"講 三角比と図形の性質 !数学的な技能 ある図形の面積がわかっているとき、その図形の面積や体積を相似比をもとにして求め ることができる。 数量や図形などにつ いての知識・理解 相似な図形の相似比と面積比及び体積比や、それらの関係について理解することができ る。




無料 中3数学 標準問題 解答プリント 328 図形の相似3 線分の比




数学 最重要 高さ共通 と 相似 面積比 集中特訓 2 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
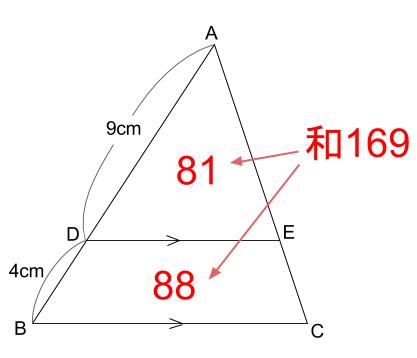
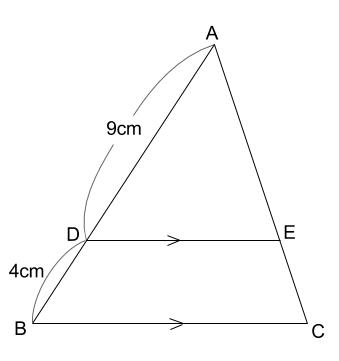
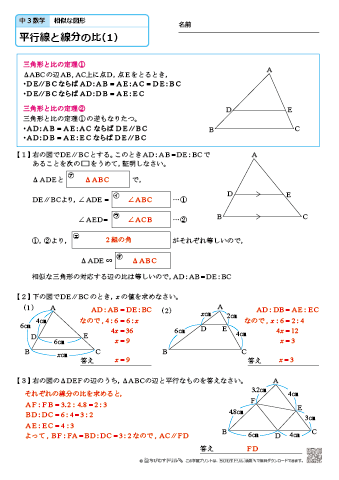
相似図形については,3組の辺の比が等しくなる. ⇒ この公式を使って辺の長さを求めることができる. ABDC=AEDE=BECE が成り立つ. もちろん, これは辺の長さが BE=3 とか CE=2 などということではない .比が 32 ということは,実際の長さとしては 6 と 4数学Ⅰ「図形と計量」<三角比の相互関係> (2)学習内容 ア 三角比の相互関係 (3)教材の目的 ① 帰納的に法則を見出す力の育成 ② 出された意見の正当性に関する議論活動 ③ 三角比の相互関係に関する定理の理解の深化 (4)指導時期案相似な図形は 対応する部分の 長さの比 は全て等しい。 対応する角 の大きさはそれぞれ等しい。 このときの対応する部分の長さの比を 相似比 という。 例) ②は①を15倍に拡大した図形である。 a b c d e f g h ① ② 15倍に拡大した図形なので、 相似比は115=23である。
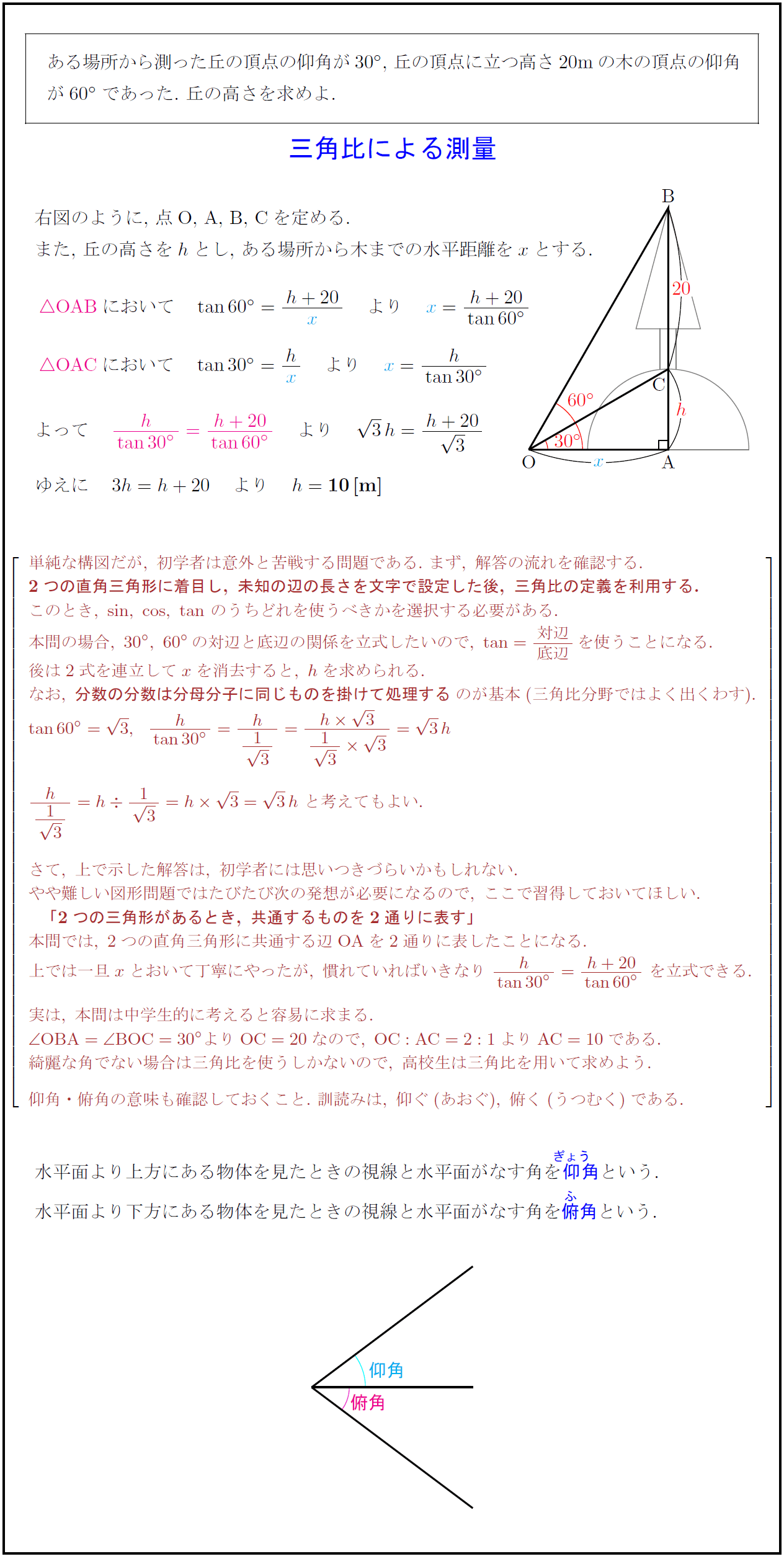



高校数学 三角比による測量 仰角と俯角 受験の月




図形と計量 三角比 頻出図形問題 凝縮一目瞭然チャートを公開 数学 化学講師 佐藤学による受験生に役立つ濃縮ポイントと Etc
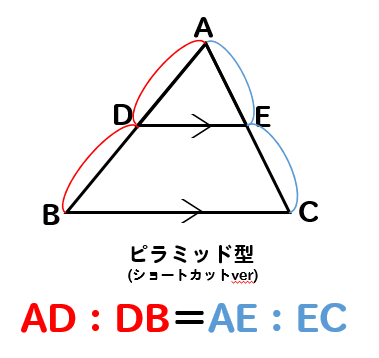
中学数学相似の重要形 ピラミッド型と砂時計型 中学数学平行線と線分の比・その1 中学数学平行線と線分の比・その2 中学数学中点連結定理 中学数学相似な図形の面積比 中学数学相似な図形の体積比 中学数学直角三角形の中学3年生 数学 三平方の定理 練習問題プリント;18/6/19 高校数学A 平面図形 スポンサーリンク 平面図形は受験における位置づけが難しい分野である。 重要か否かと聞かれたら重要であると答えざるを得ない。 大学入試共通テストでは平面図形が1つの大問として出題される ことが決まっているからである
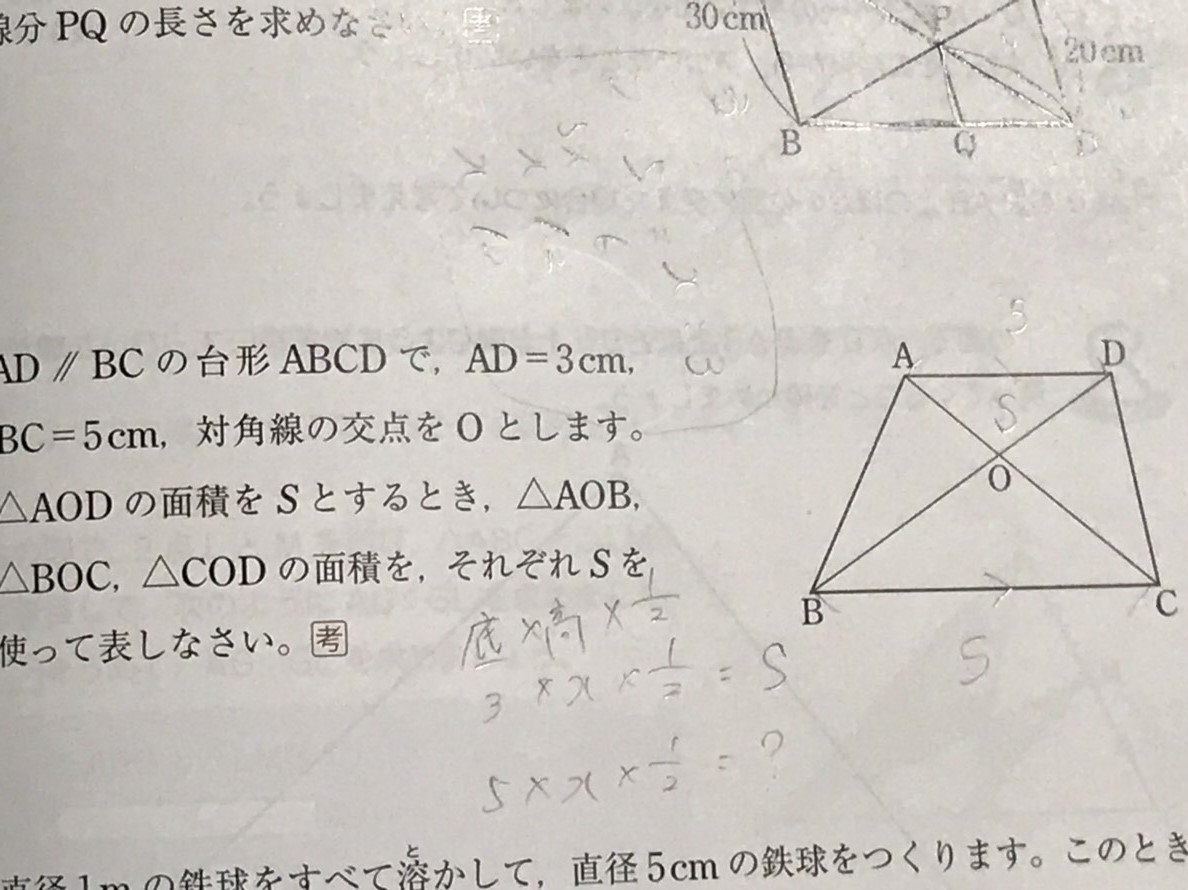



面積比




図形の面積比 体積比 数学i フリー教材開発コミュニティ Ftext
平行線と線分の比 図形と相似 Try IT(トライイット)の平行線と線分の比の問題の様々な問題を解説した映像授業一覧ページです。中学3年生 数学 相似な図形 練習問題プリント 無料ダウン数学A /図形の性質「平面図形」 5 / ??
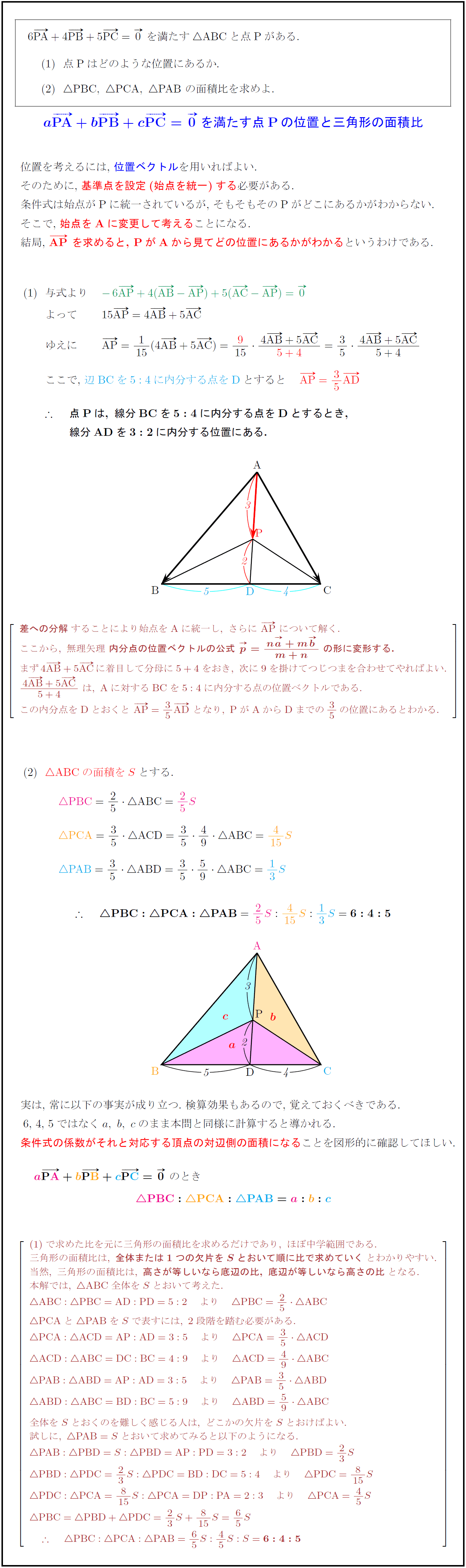



高校数学b Apa Bpb Cpc 0を満たす点pの位置と三角形の面積比 受験の月



中3数学12 図形の相似3 線分の比 発展問題プリント 問題 328
2つの図形は相似になっており ab:cd=6:9=2:3より 相似比は2:3だと分かります。 つまり、他の辺の比も2:3になるので ae:de=be:ce=2:3 とわかります。 このae:de=2:3ということを利用して 次は、 adbと edfに注目すると相似な図形に気付き,相似条件を用いて2つの三角形が相似であることを証明している。また,相似 比を利用して比例式をつくり,その求め方を説明している。 ア 数学への 関心・意欲・態度 イ 数学的な見方や考え方 ウ 数学的な技能 エ 数量や図形なこちら の記事で説明したように、 三角形の面積比は「(底辺の比)×(高さの比)」 で求めます。




世界一わかりやすい数学問題集中3 5章 図形と相似



中学生数学相似な図形の相似比と面積比について画像の正方形abcdで 辺bc Yahoo 知恵袋




相似 平行線と比の利用 辺の長さを求める方法をまとめて問題解説 数スタ
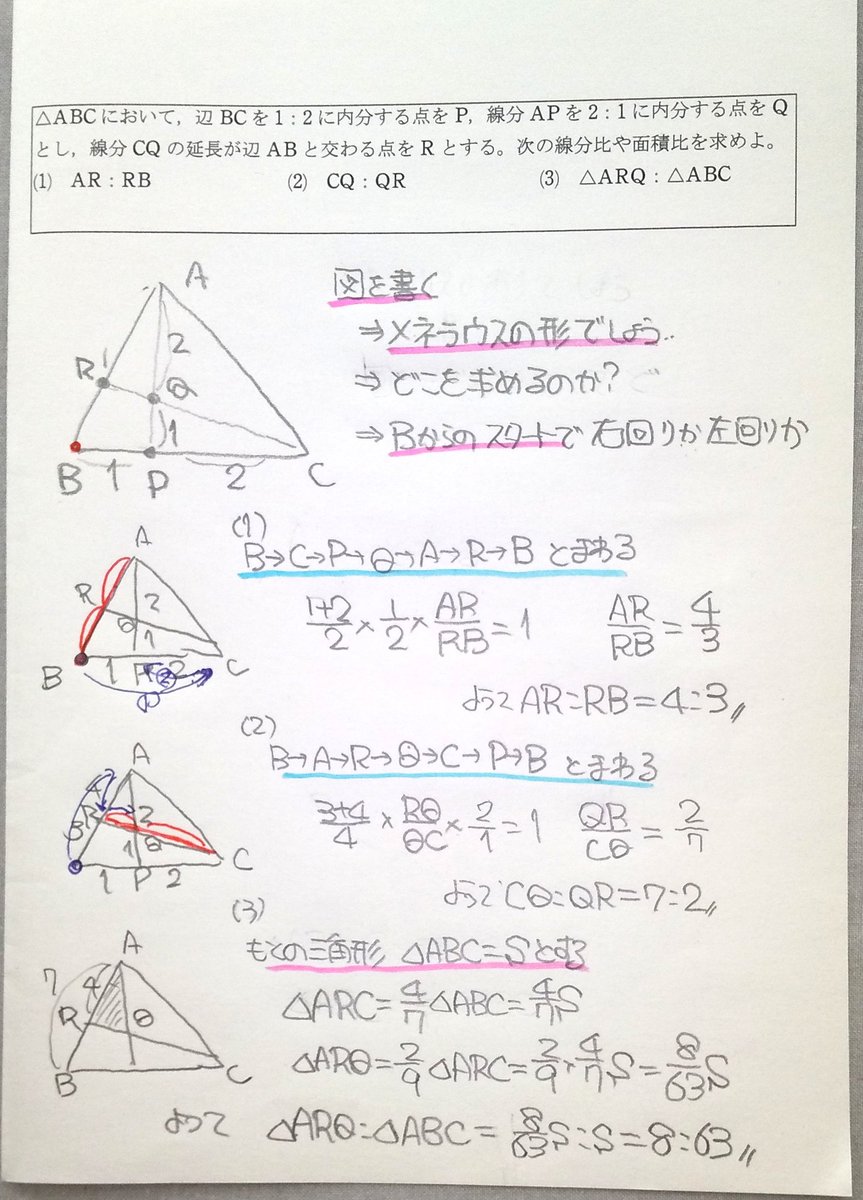



原田 浩明 على تويتر Sサクシード064 チェバの定理 図形が上手く書けないとき メネラウスと三角形の面積比 高校 数学 1年 数学a 図形の性質 チェバ メネラウス




相似 平行四辺形と面積比の問題を徹底解説 数スタ




数学 面積比と線分比をシッカリわかると チェバの定理を深く理解できるよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生



中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su



中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su
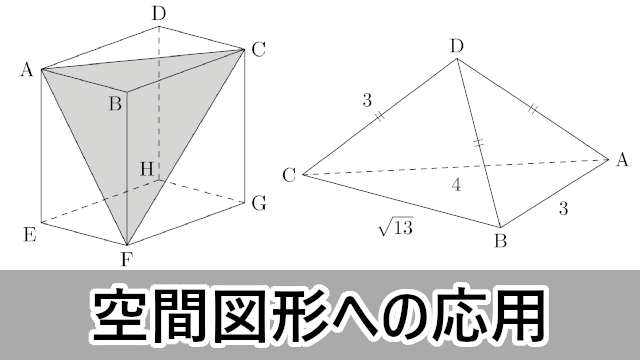



数学ia 空間図形の応用問題 広島工業大 東京慈恵会医科大 大学入試数学の考え方と解法




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




高校数学a メネラウスの定理2 応用 練習編 映像授業のtry It トライイット




相似比を使って辺の長さを求める Youtube




中学 数学 テクニック 三角形の面積比を使って辺の比を出す 高校入試 高校受験 裏ワザ Youtube
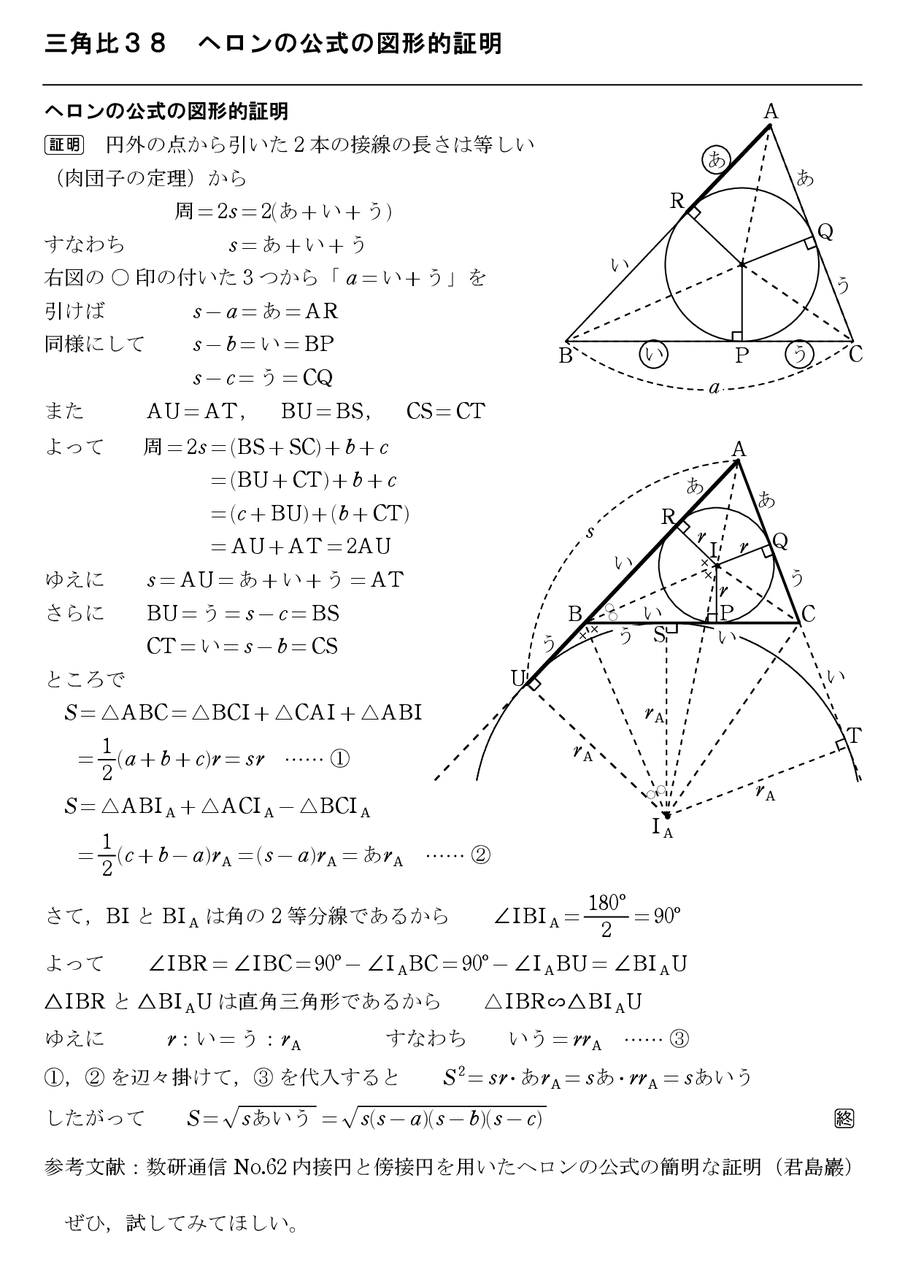



三角比38 ヘロンの公式の図形的証明 怜悧玲瓏 高校数学を天空から俯瞰する




中学数学の三角形の相似 相似条件 図形の証明と相似比 面積比 リョースケ大学




高校 数学a 図形16 面積比と線分比 12分 Youtube



数学 なぜ面積比は苦手になりがちなの 面積比 集中特訓 1 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
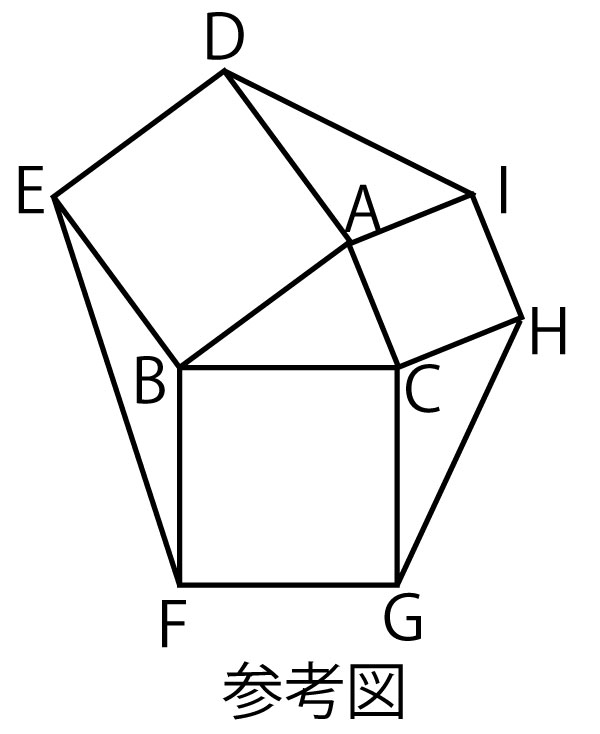



21年大学入試共通テスト 数学ia 第1問 2 図形 三角比 余弦定理 正弦定理など 配点点 問題 解答 解説 船橋市議会議員 朝倉幹晴公式サイト




平面図形の苦手を解消 三角形の面積比 基本編




高校入試数学 入試によく出題される代表的パターンまとめ



子どもを混乱させる相似な三角形の2つの面積比 算数数学が苦手な子専門のプロ家庭教師みかん先生




図形の面積比 知っている人は5秒以内には解ける面積比の裏技 暇つぶしに動画で脳トレ




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




中学校数学 証明のコツ 入試で差がつく 面積の比 体積の比 を得意にできる教材



中学数学 相似な図形の面積比 中学数学の無料オンライン学習サイトchu Su




平面図形をマスター 三角形の面積比 応用編その3




中3数学 相似と線分比1 平行四辺形 Youtube




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ




数学 平行 と 線分比 の関係についてまとめました 知っておくと応用がきくよ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生
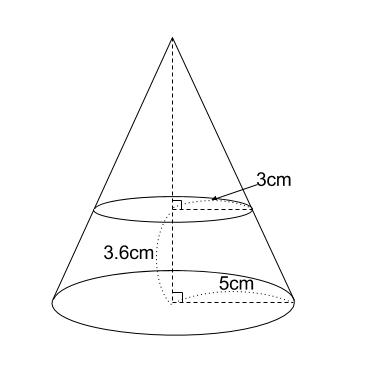



中学数学 相似な図形の体積比 中学数学の無料オンライン学習サイトchu Su




図形の面積比 知っている人は5秒以内には解ける面積比の裏技 Youtube



3



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
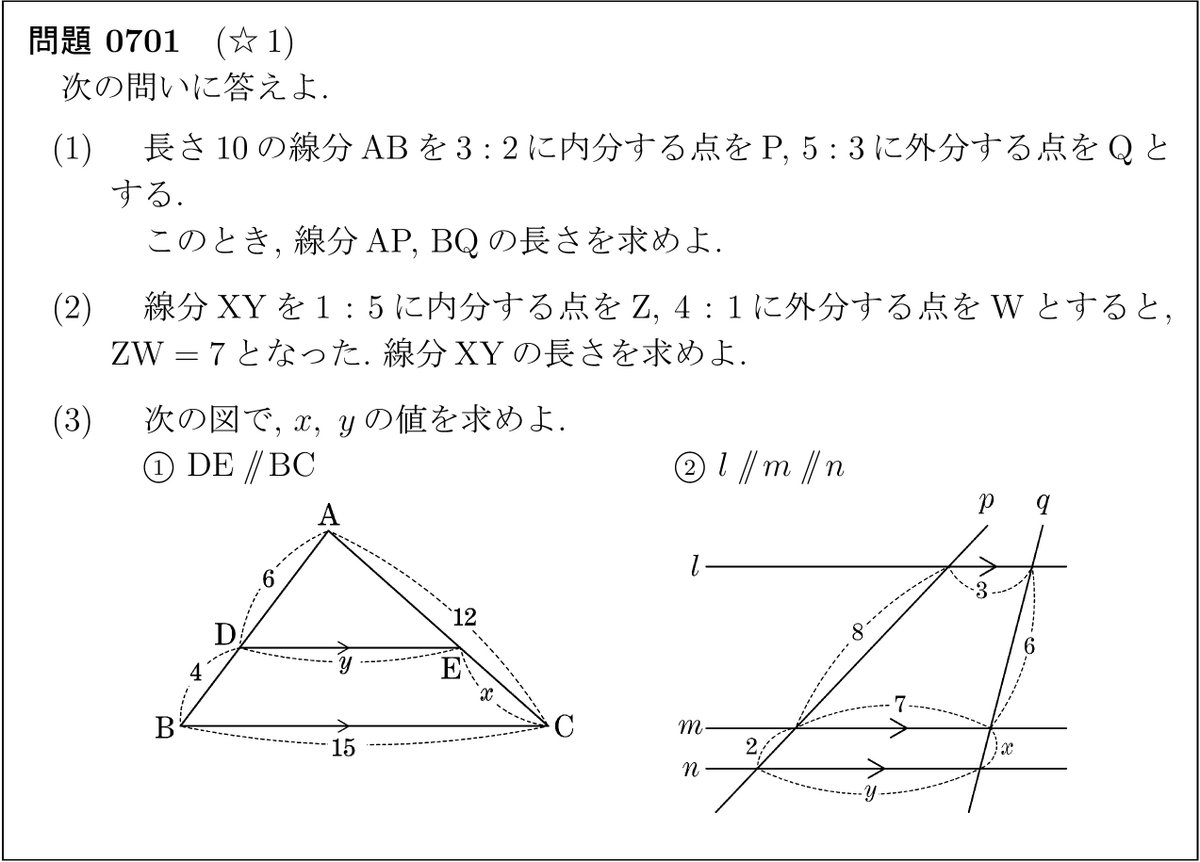



高校数学基本問題垂れ流し 07 図形の性質 1 三角形と比 線分の内分と外分 平行線と比 T Co Rvv5doaz7m




中学受験の 面積比 は2種類 似ていても性質が全く異なるので注意 中学受験ナビ



三角形の面積比をてんびんで解く 中学受験プロ講師ブログ




相似な図形 面積比の問題 苦手な数学を簡単に




高校数学a 方べきの定理3パターンの証明と三角形の相似 受験の月




3分でわかる 相似比から面積比の公式 Qikeru 学びを楽しくわかりやすく




面積比の公式まとめ 相似比と面積比と体積比の関係もあわせて解説 遊ぶ数学



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su




世界一わかりやすい数学問題集中3 5章 図形と相似




数学 中3 49 平行線と線分の比 基本編 Youtube




数学 三角形の辺と面積の比について 2つの考え方をサクッとまとめました 中学数学 図形 行間 ぎょうのあいだ 先生




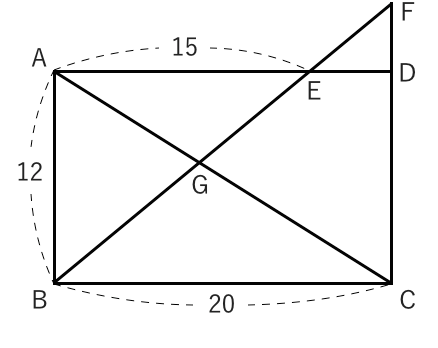
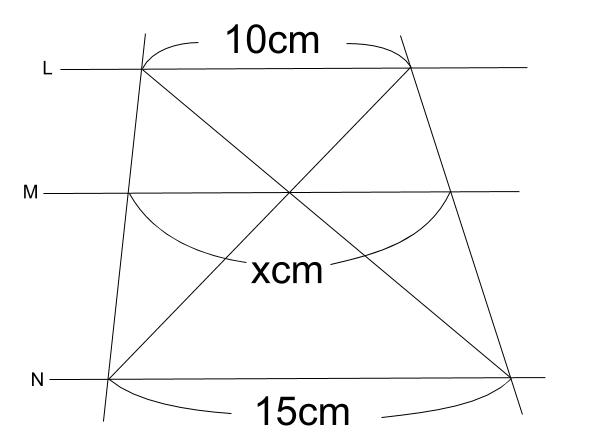
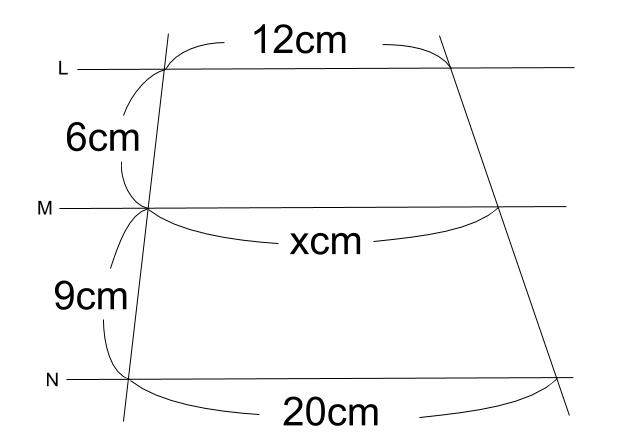
なぜ 周の長さの比は 25を使うんですか 下の15cmは使わないんですか Clear



Studydoctor相似比と面積の計算 中学3年数学 Studydoctor




中3数学 図形と相似27 相似な図形の面積比 すべて無料 星組の中学数学講座




数学 チェバの定理 とは 定理の覚え方や問題 例題 証明 面積比との関係などをまとめました チェバの定理の逆もどうぞ 平面図形 中学数学 高校数学 行間 ぎょうのあいだ 先生




高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月




公立高校入試直前図形問題対策 線分比の出し方 京橋数学塾a4u
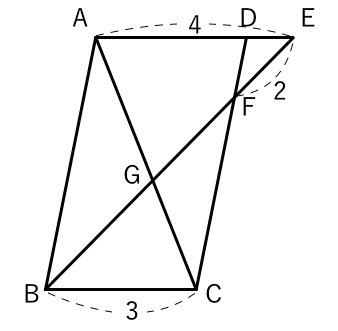



相似な図形 平行線と線分の比 平行四辺形 苦手な数学を簡単に




相似な図形 補助線を引いて考える相似の問題 中学生からの勉強質問 数学 進研ゼミ中学講座
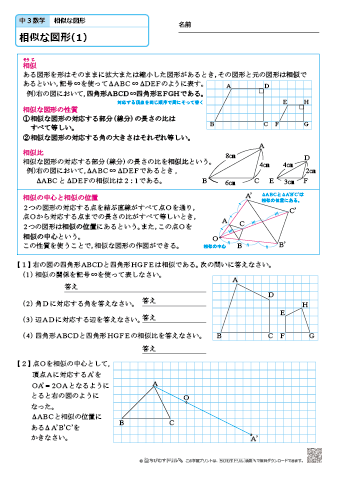



中学3年生 数学 相似な図形 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
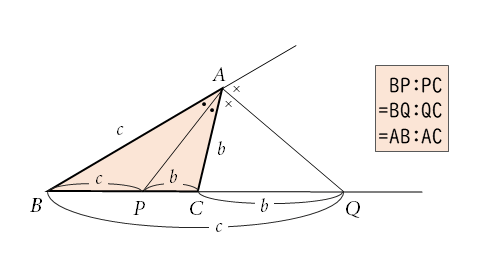



数学の公式 定理集 図形の性質 日々是鍛錬 ひびこれたんれん




世界一わかりやすい数学問題集中3 5章 図形と相似



1
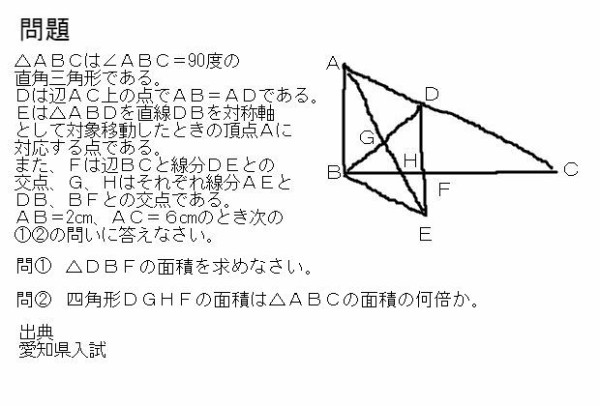



図形総合問題 辺の比利用のみでの解法 中学数学 理科 寺子屋塾の復習サイト
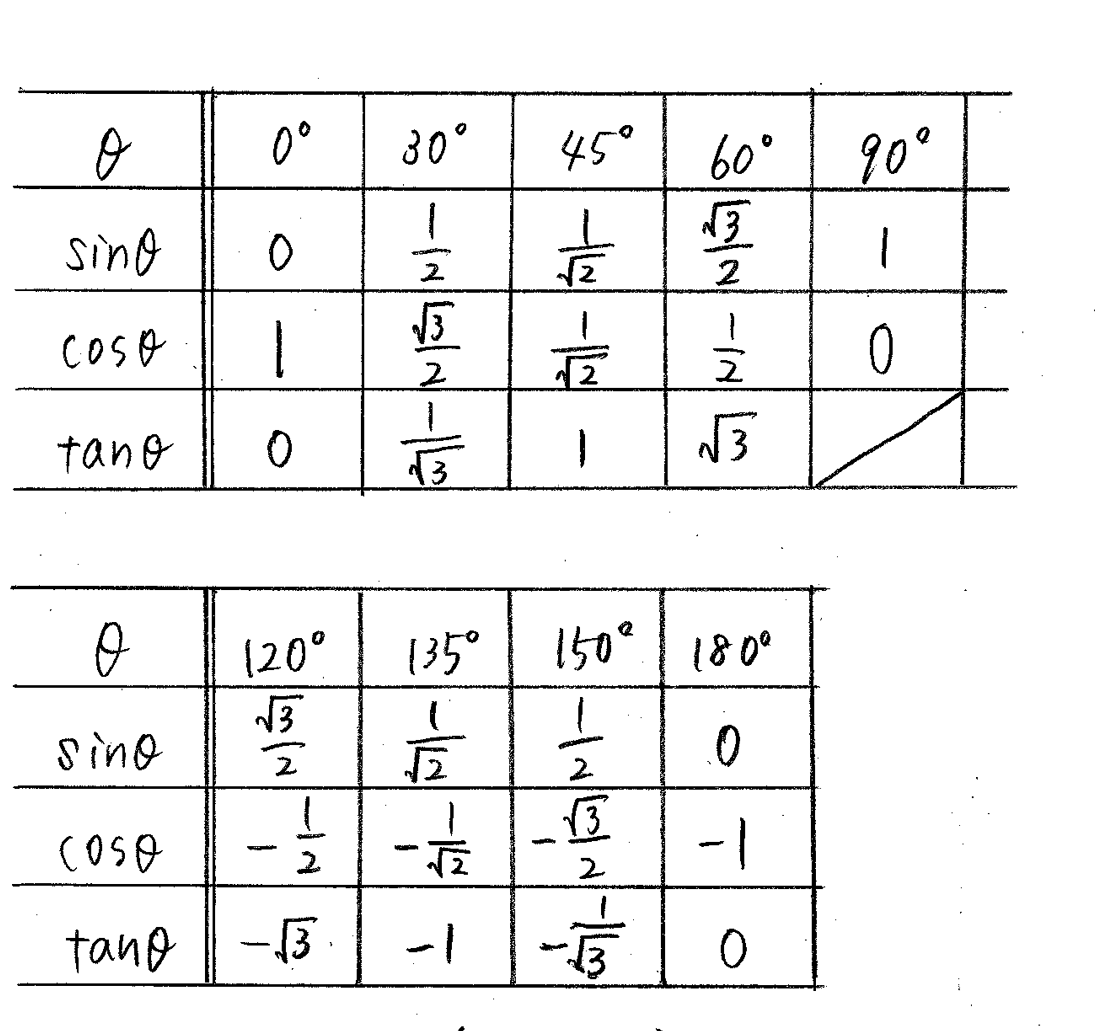



改訂版 クリアー数学 P69 23 三角比の拡張



1
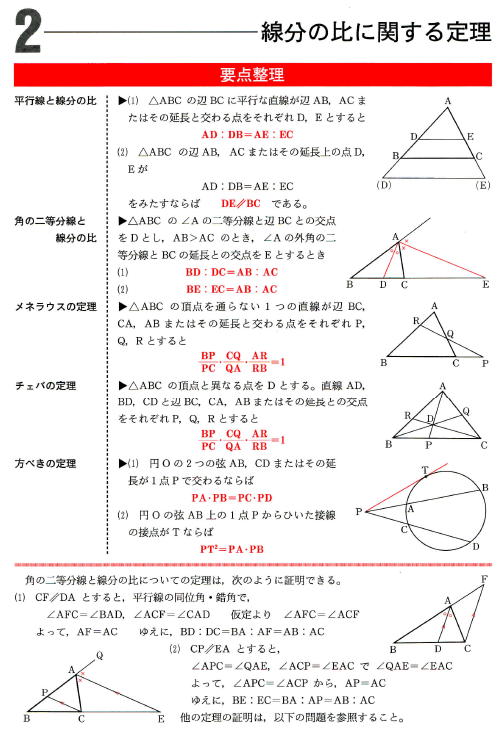



図形の性質 線分の比に関する定理 数学 さくら教育研究所 Skredu




三角形の相似条件と証明問題の解き方 数学fun
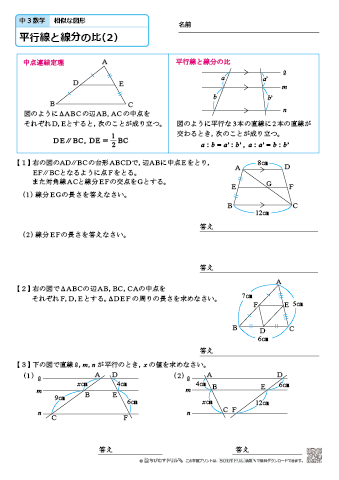



中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生
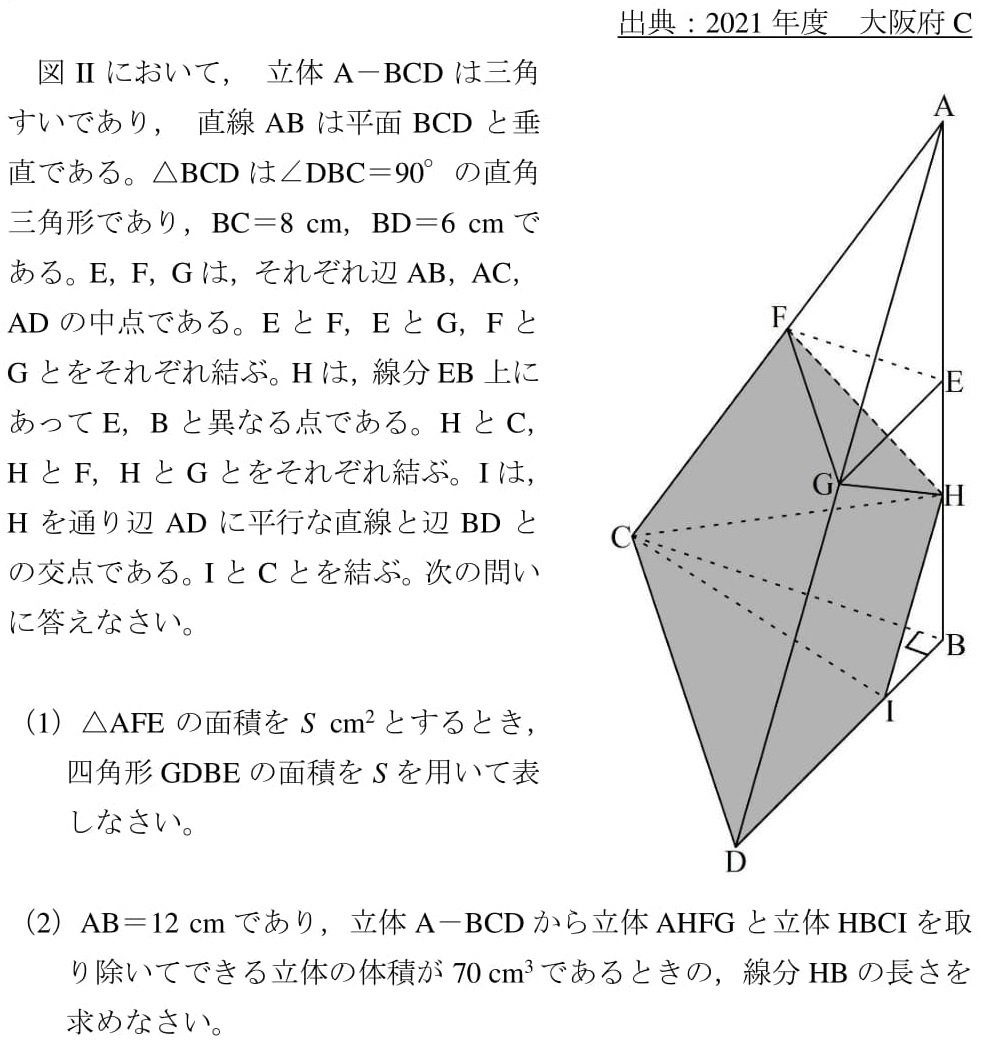



21年大阪府c 相似と面積比 体積比の練習 高校入試 数学 良問 難問




高校入試数学 相似の比合わせ 連比の問題




相似な図形の面積比の問題 相似比を出してから二乗しよう 中学や高校の数学の計算問題




高校入試数学 相似の比合わせ 連比の問題



三角形の面積比を求めよう 底辺比と相似比を使えば複雑な問題もスッキリ解決 中学受験ナビ



中学数学 平行線と線分の比 その2 中学数学の無料オンライン学習サイトchu Su



Studydoctor相似な三角形の辺の比 中3数学 Studydoctor




平面図形をマスター 三角形の面積比 応用編その3



数学 台形を4分割した図形パターン 面積比 集中特訓 3 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo




数学a 平面図形 三角形の辺の比の問題です 下の図 添付画像 にお 数学 教えて Goo




中学3年 数学 東京書籍 新しい数学 相似な図形 平行線と比 赤城 ᐡᐤᐡ




辺の比 面積比 相似 16年東京都 高校入試 数学 良問 難問




中3数学 相似な図形の表面積比 体積比 映像授業のtry It トライイット



1




中学3年生 数学 平行線と線分の比 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学3年数学練習問題 三角形の比 辺の長さを求める問題 図形と相似




数学a 図形の性質 以下の問題の解説赤線部について 相似条件は 3辺が等しい Clear




中3数学 図形と相似23 平行線と線分の比 比の合成 連比 すべて無料 星組の中学数学講座




改訂版 坂田アキラの 三角比 平面図形が面白いほどわかる本 坂田アキラの理系シリーズ 坂田アキラ 本 通販 Amazon




大学入試 苦手対策 三角比 平面 空間図形 に強くなる問題集 旺文社




苦手を克服 数学aの平面図形で使う定理の一覧 数学a By となりがトトロ マナペディア




底辺の比と面積比 中学2年生 図形 数学 Youtube



相似 平行四辺形と面積比の問題を徹底解説 数スタ



中学数学発展 シンプルだけど難しい ラ サールの難問 平面図形 定期テストや高校入試に レオンの中学数学探検所




平面図形をマスター 三角形の面積比 応用編その3



0 件のコメント:
コメントを投稿