一筆書きの書き方は何通りあるか(フェリス女学院中学 05年) 線からエンピツを離さずに、同じ線を1回しか通らないで形を描くことを一筆書きといいます。 たとえば、下の図1を点A から始めて一筆書きする仕方は、左回りと右回りの2通りあります。 3分で分かる!最大公約数の意味・3通りの求め方をわかりやすく! 数学 425 3分でわかる!漸化式の解説・問題の解き方をわかりやすく 日本史 金融恐慌と山東出兵上記の通り、mを3回かければ、立方メートルになります。立方メートルの単位の記号は、「m 3 」です。立方メートルの意味は、下記が参考になります。 m3(立米)とは?1分でわかる意味、読み方、求め方、単位換算、トンとの関係
A B Cの組み合わせは8通りですが これは自分で書き出す以外どのよう Yahoo 知恵袋
何通り 求め方 高校
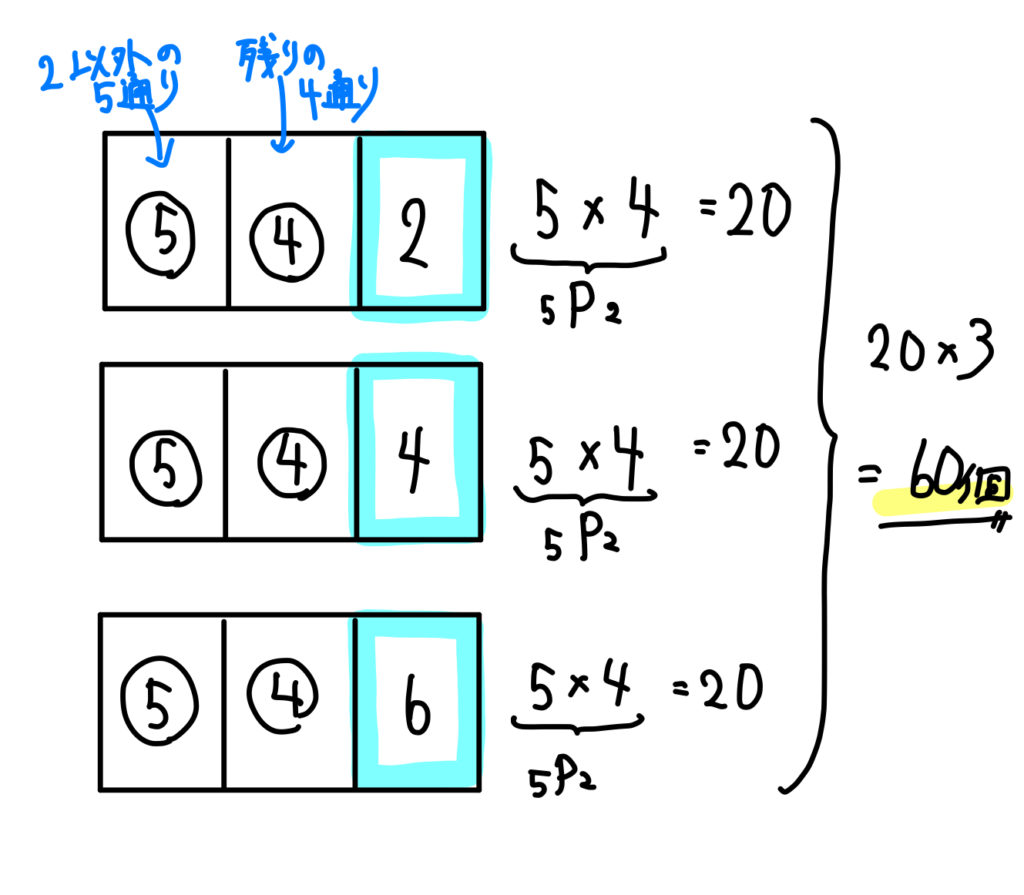
何通り 求め方 高校-解説 右の図のような樹形図を使って考えると、 Aが左はしにくる場合、4×3×2×1=24通りあり、 B、C、D、Eが左はしにきたときも同じなので、 全部で5×24=1通りになる。 A-BとB-Aで2通りとする場合を順列という。 N個のものを1列に並べるとき、その並べ方は N×(N1)×(N2)××2×1 という基本の公式がある。(通り) となるので, (1) で求めた点 a から点 b までの最短経路の総数からこれを引くことで (通り) と求められます。 (3) (2) と同様に余事象の考え方を用います。



組合せと順列は何が違うのか 組合せは樹形図でも計算でも解ける
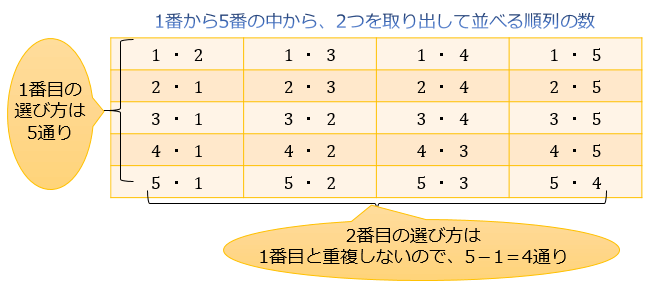
回答数: 2 件 大変お恥ずかしいのですが『何通りあるかの計算』について教えてください。 小学5・6年で習ったのですが、年近く経過して、すっかり忘れてしまいました。 1:『何通りあるかの計算』は、なんと言う名前なのでしょうか。 2:一般的な計算式を教えてください。 赤・青・黄・白・緑の5色の色鉛筆が1本ずつあるとして・・・ 5色の色鉛筆 ここでは、部分的に順序が指定された状況で並び方を数える問題を見ていきます。 例えば、「AさんがBさんより左にくる並び方は何通りあるか」のような問題を見ていきます。 順列ですが、使うのは組合せです。 その点では、 標準同じものを含む 3 ビットなら 2 × 2 × 2 = 8 通り になるのです。 ビット数だけ 2 を掛ければよいのです。 このことから、 8 ビットなら、2 を 8 回掛けて、 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 256 通り だとわかります。 何度も掛け算をする式を書くのは面倒なので、べき乗の表現を使うことにしましょう。 たとえば、8 ビットで表せるビットパターンは、2 を 8 回掛けるので 2 8
日常場面からタンジェントを学ぶ:傾きから角度を求める タンジェントは 角度と(直線の)傾きをつなぐ 重要なものです。 例として、坂道の傾斜角度を求めてみましょう。 皆さんはこんな標識見たことありませんか? これは 100m進んだ時、9mだけ高さ両親が隣り合うのは,両親を 1 組とした 5 人の円順列で,両親の座り方が 2!_____ aaa の並べ方 → 1 通り でも求められる. の文字を並べ替えてできる順列のうち, 314ab2c のように a,b,c はこの順に並んでいるものは何通りあるか. 12 18 35 36 38
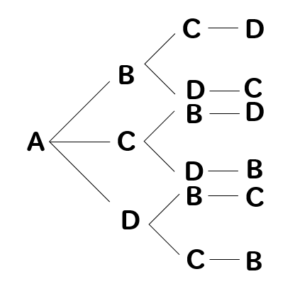
求められます。更に,bの1個手前までの経路数を知るには, もう1個手前までの経路数が分かれば良いですね。 そうやってどんどん遡っていくとやがて始点aに辿り着きます。 そこで, aから各交差点までの経路数を始めの方から順に図に書き入れて いけば で答えは6通り 検証 下記がその6通り abc acb bac bca cab cba (2)英数字のみのパスワード4桁 アルファベットは26文字 数字は10種類 同じ英数字を二度使ってもかまわないので 選べる英数字は毎回36通り ここから4桁を選ぶのだから 36×36×36×36= 通りサイコロを何回かふって出た目の数の和が4になるのは何通りありますか。 → 解答 問題21 次の(1)から(3)の図形は、一筆書きが可能かどうか答えなさい。 → 解答 問題22 次の図形を一筆書きした場合、何通りの書き方があるか求めなさい。



Aからbまで最短距離で移動する方法は何通りか という問題で Yahoo 知恵袋



組み合わせ C とは 公式や計算方法 は何通り 受験辞典
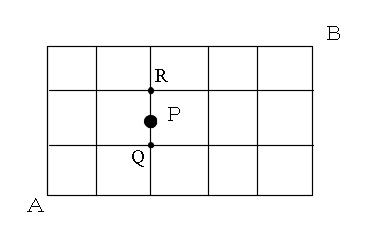
通行止めを通るやり方を数える。 スタートから点Pまでの行き方は「↑3つ→3つ」の並べ替えなので 6 C 3 =通り。 点Qからゴールまでの行き方は「↑1つ→2つ」の並べ替えなので 3 C 1 =3通り。 よって通行止めを通るのは×3=60通り。硬貨の表,裏の出方は,全部で何通りありますか。樹形図をかいて求めなさい。 答え (2) 2枚とも表となる確率を求めなさい。 答え (3) 1枚は表で,1枚は裏となる確率を求めなさい。 答え 確 率⑥ 確率の求め方 (2) d 学 年 2年 年 組 氏名たとえばいつ、どこで、なにをしたという文を作るとき いつ 昨日 さっき いつか どこで 学校で 家で 公園で 何をした くしゃみをした 爆発した 疲れた というかんじに組み合わせを作る場合って、何通りできるかってどうやったら求められますか?




この問題は何通りあるか教えてください またこの問題の場合は Pであってますか Clear




中学生2年の場合の数がわかりません 大問6 7を教えてください Clear
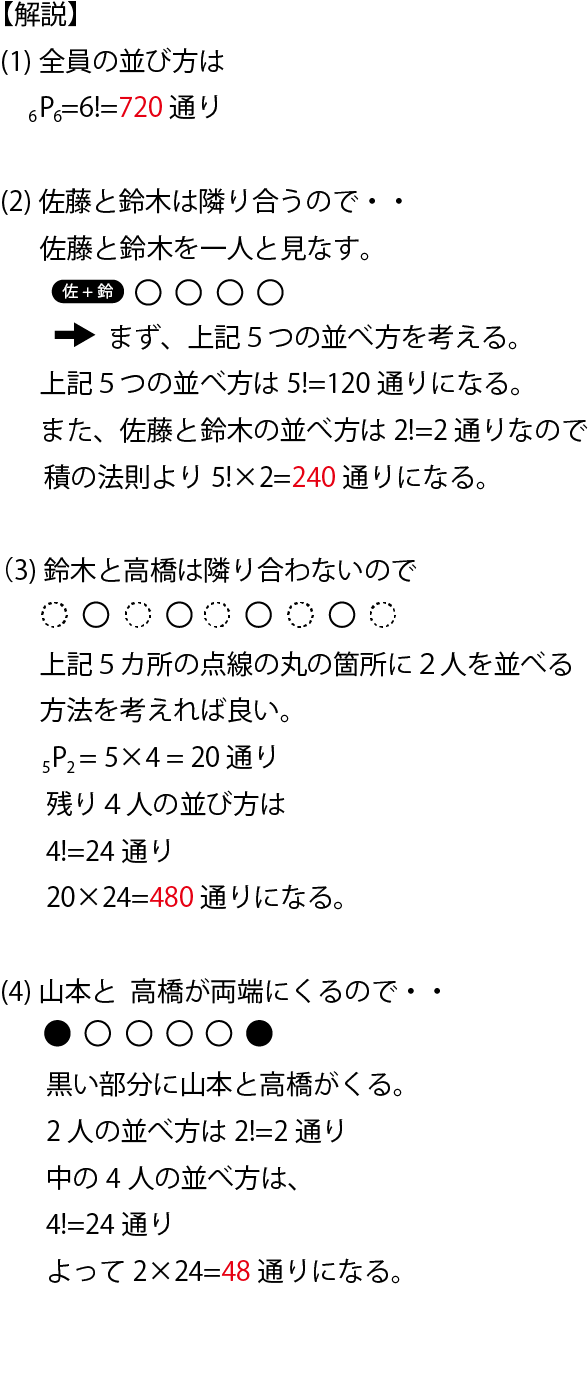
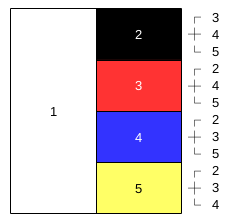
確率⑥ ~確率の求め方(色玉)~ 1赤玉5個,白玉3個,青玉1個が入っている箱から玉を1個取り出すとき,次の各問に答えなさい。 (1)玉の取り出し方は,全部で何通りありますか。 (2)青玉が出る確率を求めなさい。 人の並び方 男子5人、女子4人が1列に並ぶとき、次の並び方は何通りあるか。 女子4人が続いて並ぶ。 どの女子も隣り合わない。 両端の少なくとも一方が女子になる。 ① 女子4人を「ひとまとめ」にする。さらにその中での並びかえる。るとき、何通りの塗り方がありますか。ただし、使わない色があって もよく、隣り合う部分は異なる色に塗るものとします。 3 下の図の4つの部分に、赤、青、黄、緑の4色から何色かを使って色 を塗るとき、何通りの塗り方がありますか。



高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ




組み合わせ C とは 公式や計算方法 は何通り 受験辞典
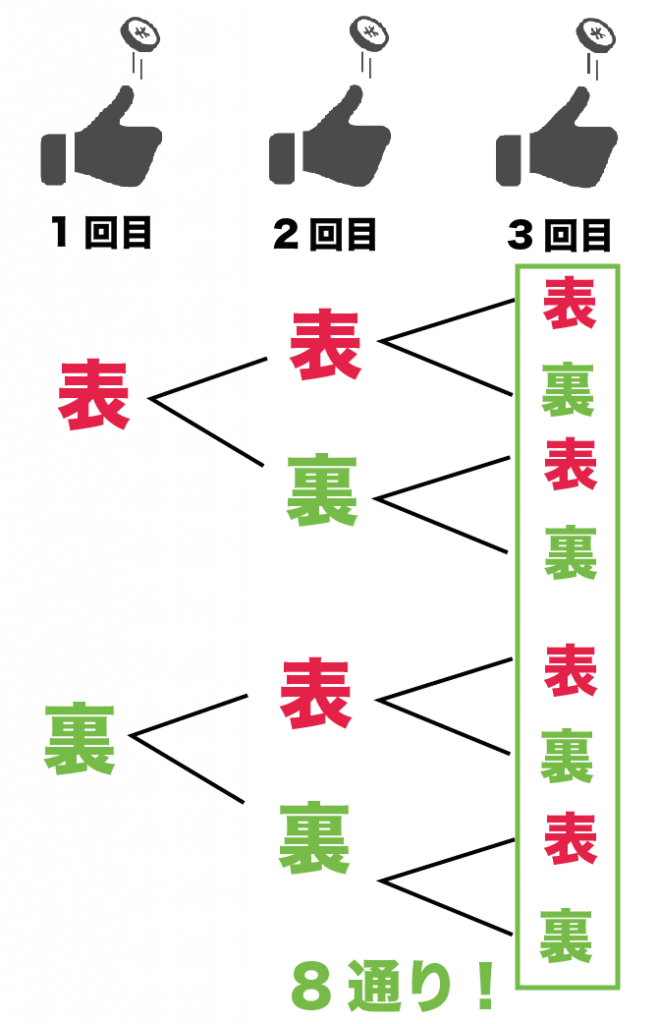
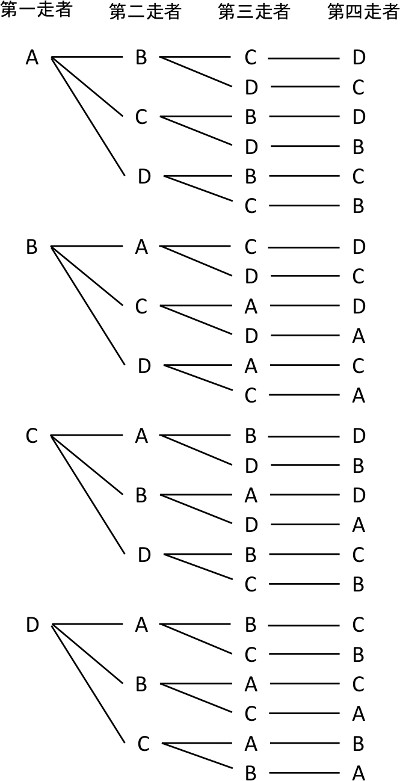
確率の公式・計算式は正直、たくさんある。 だけど、中学数学ではたった1つの公式で大丈夫。 どんな確率問題もとけるようになるんだ。 あることがら「A」がおきる確率の求め方は、 つぎの公式で計算できちゃうよ。 (Aが起きる場合の確率) = (ことがらAが起きる場合の数)÷(すべての場合の数) だ。 もうちょっと公式っぽくしたい。 そんなとき コイン投げから分かる二項分布。 正規分布やポアソン分布との関係性と近似について コインを投げると、 試行結果は基本的に「表」か「裏」かの2通り だけですよね。 このように、試行結果が「〇 か × か」や「成功か失敗か」といった2種類しかない選び方は何通りありますか。 ②12人の選手の中からリレーの3人を選ぶとき、選び方は何通りありますか。 2つの文の違いは何かな?順番を考えるのはどっちかな? 例題2 12人の選手の中からリレーの第1走者、第2走者、第3走者の3人を選ぶと




中学2年数学 確率 場合の数が分かれば確率が分かる 数学の面白いこと 役に立つことをまとめたサイト



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ
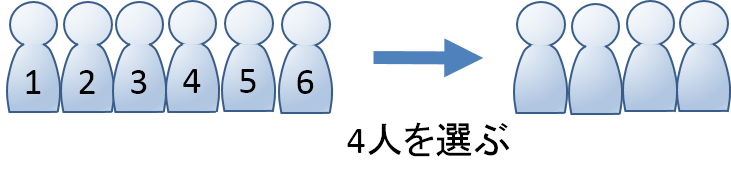
今度の分け方は、人数が同じになっていますが、 組に名前がついていることから3組は区別できると判断します。 組が区別できる場合には、Cを使って順に計算していけばOKです。 まず、9人の中から3人を選ぶ。 ⇒ 次に残った6人の中から3人を選ぶ。 ⇒ そして、最後の3人の中から3人を選ぶ。 ⇒ (必ず1通りになるので省略してOK) よって、 何かを選ぶ(だけ) 組み合わせを求めろと書いてある など つまり、 正確な位置は決めるわけではなく、選ぶだけのときは組み合わせ になり、 C C を使います。 難しい問題の場合は、直接的に「選びなさい」や「組み合わせを求めなさい」と書かれていない場合もあるので、 そのような場合は、 問題文から「選べば求まる」や「組み合わせを求めればいい東に移動することをe (eastの略),北に移動することをn (northの略)で表すと,右の茶色の順路はeneenenに対応しており,青の順路はnneeneeに対応しています eが4個,nが3個 (同じものが)あるときの順列 の総数を求めれば,それが順路の総数になります (答案) =35通り・・・(答) 余談1 右図のように,平行線の幅が異なる場合でも,上の答案でよい:それぞれの



1



Air Repo Nii Ac Jp Action Repository Uri Item Id 4691 File Id 22 File No 1
通りとなります。ここで,5人から3人を選ぶ選び方(つまり組合せ)の数を仮に m とします。すると,5人から3人選出し並べる並べ方は,上のように1つの組に対し 3!通りより (通り) よって, (ア) で求めたすべての座り方から両親が隣り合う座り方を引くことで, 両親が隣り合わないのは (通り) と求められます。 Python こんにちは! 皆さんは、 順列や組み合わせを求めよう と思ったことはありませんか? itertools を使えば簡単に求めることができますよ。 今回の記事では、itertoolsを使った以下の方法について紹介します。 順列を全通り表示する方法 順列が何通り




組合せと順列は何が違うのか 組合せは樹形図でも計算でも解ける



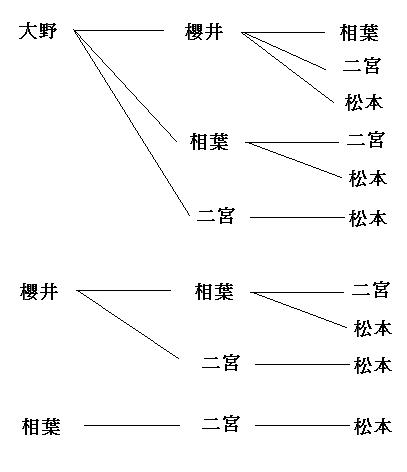
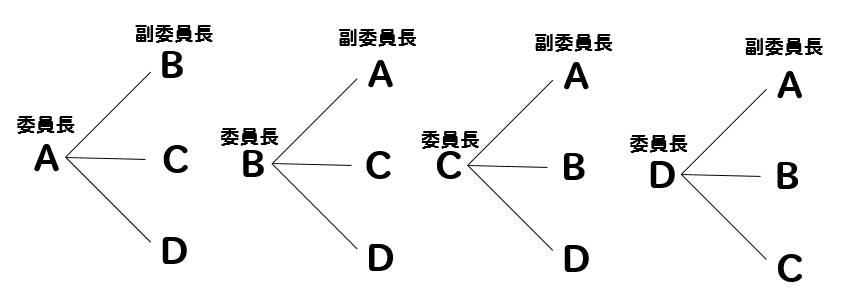
確率の問題です A B C D Eの5人から3人の委員を選ぶとき 何 Yahoo 知恵袋
円周の求め方・円周率とは何か・なぜ無限に続くのかを説明。 その割り切れない理由について 14m件のビュー 分数の割り算はなぜひっくり返してかけるのか? COMBIN 組み合わせの数を求める 対応バージョン: 365 19 16 13 10 総数個の項目のなかから抜き取り数個を取り出したとき、何種類の組み合わせが可能であるかを求めます。 二項係数を求めることもできます。確率④ ~確率の求め方(コイン)~ 13枚のコインを同時に投げるとき,次の各問に答えなさい。 (1)表裏の出かたは,全部で何通りありますか。 (2)3枚とも表になる確率を求めなさい。 (3)2枚は表で1枚は裏となる確率を求めなさい。




中学生です この数学の確率の問題についてなんですが と が分かり 数学 教えて Goo




この問題の3番の求め方教えてください ちなみに答えは36通りです Clear
男子5人, 女子3人が一列に並ぶとき, 男子が両端になる並び方は何通りあるか求めよ。 解答 この問題は順番が関係あるので順列 両端の男子の選び方は ←条件処理 5 p 2 = この間に、残りの6人を並べるので 6 p 6 =6!=7 よって、求める場合の数は 6人が円形のテーブルに座った時の座り方は、円順列という考え方で求められます。 横に6人の並び方は、6! (6×5×4×3×2×1)で求められますが、 円で6人が並ぶ場合は 例えば、と、、、、、の全てが同じ並び方となります。 つまり、横の並び方(6! )で求めると上記の並び方は別個に数えていますが、



中2数学 基本問題プリント12 確率4 求め方2 問題 236



立体の最短経路の求め方を教えてください Aからbまでの最短経路は何通りある Yahoo 知恵袋



A B Cの組み合わせは8通りですが これは自分で書き出す以外どのよう Yahoo 知恵袋



順列 3桁 4桁の整数をつくる問題をパターン別に解説 数スタ



3連単 5頭ボックスは何通り 計算方法は 競馬で勝つ方法 研究レポート うまめし Com 競馬必勝法




高校数学 1から分かる順列と組み合わせの違い 公式 問題付き 高校生向け受験応援メディア 受験のミカタ



中学数学 確率の求め方がわかる1つの公式 計算式 Qikeru 学びを楽しくわかりやすく




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun




上何 通り ある か 計算 小学生 子供のための最高のぬりえ



順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




場合の数 並べる と 選ぶ の計算方法の違い



Worldcupの8文字を1列に並べる時 W R C Pがこの順にある並 Yahoo 知恵袋




何通りある 順列まとめ 数学の偏差値を上げて合格を目指す




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



組合せと順列は何が違うのか 組合せは樹形図でも計算でも解ける




小学生の算数全部で何通りですがわかりません 小学6年生の親です小学 数学 教えて Goo




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun
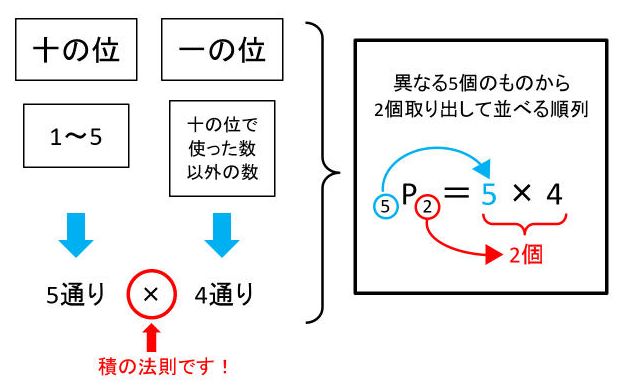



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ




何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ




中2 硬貨の確率の求め方 ポイントは 樹形図だ Youtube



順列と組み合わせの違いをリレーのチーム選考に例える コード7区




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ
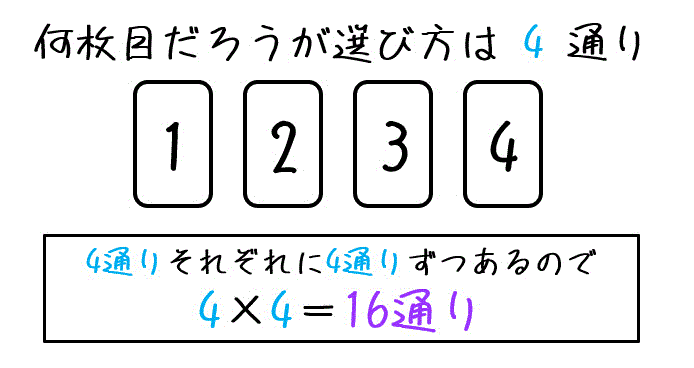



うさぎでもわかる場合の数 順列と組み合わせの違い 工業大学生ももやまのうさぎ塾




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 中学受験ナビ



場合の数 学び家 Com




場合の数 は 順列 の計算の応用 中学受験プロ講師ブログ
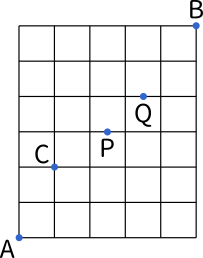



数a場合の数 最短経路の求め方 どうしてcを使うの Mm参考書
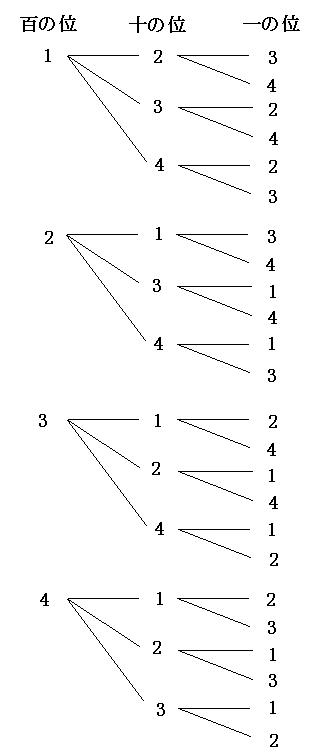



解き方解説 場合の数を計算で解く 場合の数は計算でサボれ



組み合わせの考え方と公式 組み分けと道順を求める問題の解き方



順列 3桁 4桁の整数をつくる問題をパターン別に解説 数スタ



この26番の問題で 男子が少なくとも一人含まれるときは何通りかという問 Yahoo 知恵袋




順列と組合せを理解してみる 順列 デジタル デザイン ラボラトリーな日々




3 4 5 の計算で求める方法を教えてください 答えは 3 736通り Clear




重複順列とは 基本公式と解き方を解説 高校生向け受験応援メディア 受験のミカタ




中2 硬貨の確率の求め方 ポイントは 樹形図だ Youtube
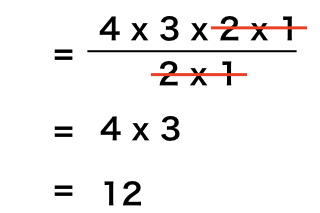



組み合わせ計算は何通り 重複も合わせる順列との違いを簡単攻略 Landgather




何通りか求める計算式わかる方いますか Clear



苦手な人向け 組み合わせcの計算のやり方を簡単にサクッと解説するぞ 数スタ



Happylilac Net Kumiawase Ans Pdf



7 3 Cの使い方 統計学の時間 統計web



7 3 Cの使い方 統計学の時間 統計web




無料 中2数学 標準問題 解答プリント 235 確率3 求め方



Q Tbn And9gcrwcnbyjcxmrexvqio6nv6s L8p7sr Ptt0dbbh Tfkgamcgurj Usqp Cau



算数 場合の数の解き方は 問題別に考え方を解説 数スタ



算数 場合の数の解き方は 問題別に考え方を解説 数スタ




無料 中2数学 標準問題 問題プリント 235 確率3 求め方1



順列と組み合わせの違いと見分け方 公式や計算問題 受験辞典
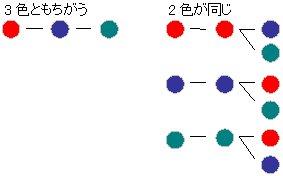



場合の数



組み合わせ C とは 公式や計算方法 は何通り 受験辞典




3連複ボックスの計算式と点数が何通りになるか調べる方法 賢い馬券の買い方




高校数学 組み合わせ コンビネーション Ncr の計算方法のコツ できるだけ楽に計算しよう 数学の面白いこと 役に立つことをまとめたサイト
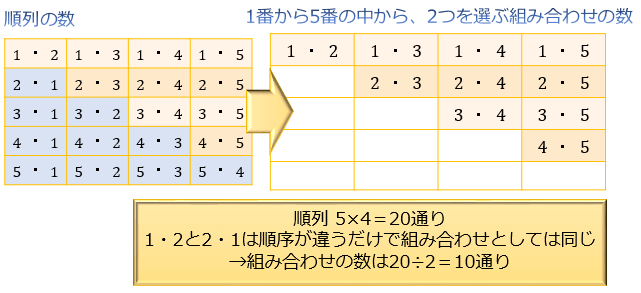



順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ




何通りかの計算で 7c4 の答えがわかりません 計算の仕方も教えて貰え 数学 教えて Goo
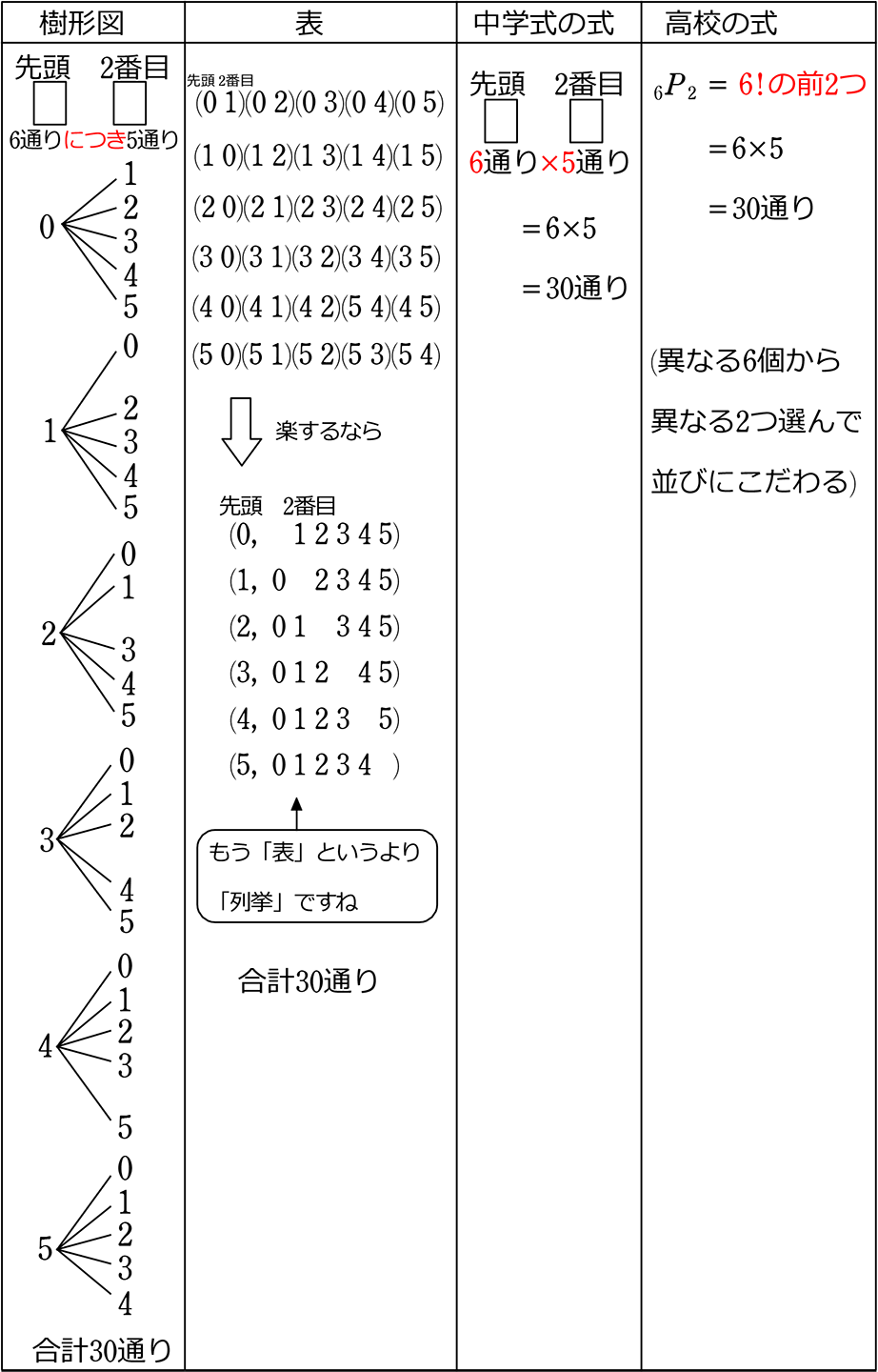



中学数学 場合の数




順列nprの計算 数学a フリー教材開発コミュニティ Ftext




ならべ方 と 組み合わせ 小学校の 場合の数 の問題の解き方 数学fun



数字の組み合わせの問題で 7人の中から3人選ぶ組み合わせは何通りあるのでし Yahoo 知恵袋
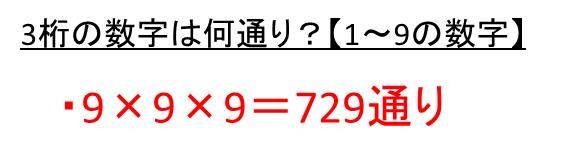



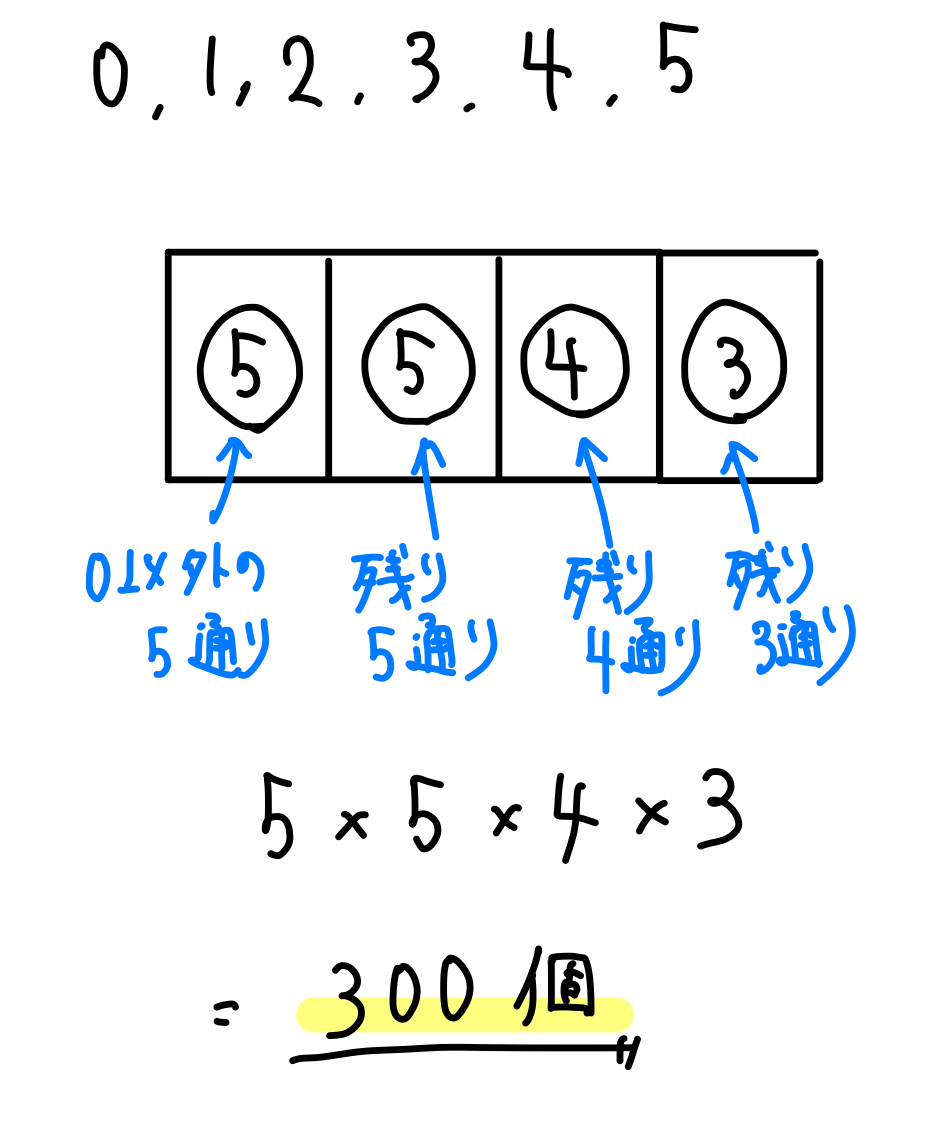
3桁の数字は何通りある 0 9や1 9の場合 5桁の数字は何通り パスワードやパスコードや暗証番号 ウルトラフリーダム



組み合わせ C とは 公式や計算方法 は何通り 受験辞典
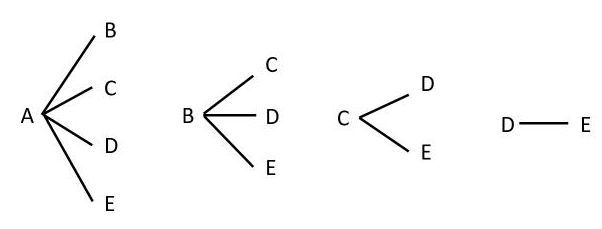



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 ページ 2 2 中学受験ナビ



何通りあるかを計算で求めよう 場合の数 が苦手な小学生のための公式の使い方 ページ 2 2 中学受験ナビ




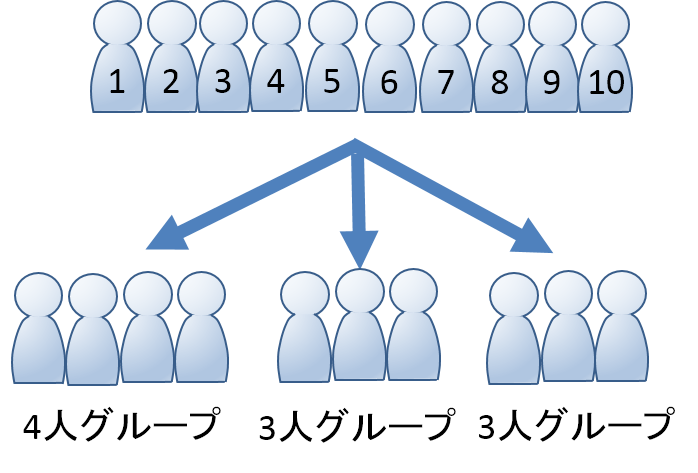
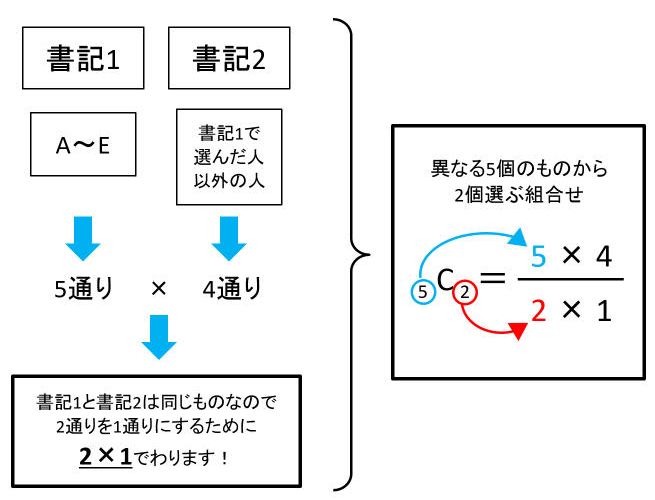
問 8人の生徒を2人 3人 3人の3つのグループに分ける分け方は何通り 大学受験 教えて Goo
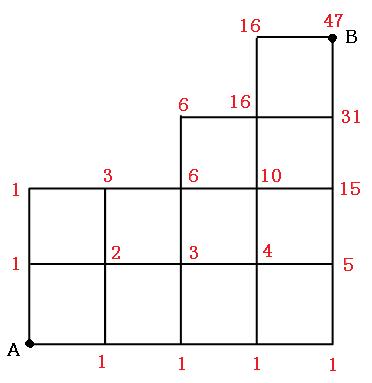



道順を求める場合の数の裏技 場合の数の道順は数字を書きこんでいけ



1
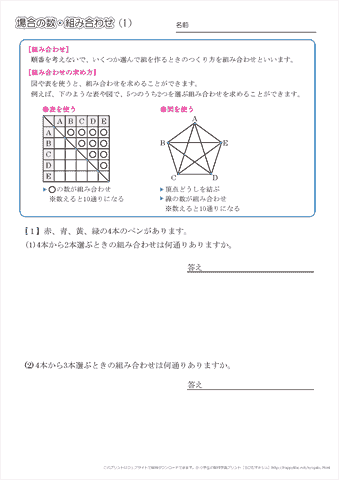



小学6年生の算数 場合の数 組み合わせ 練習問題プリント ちびむすドリル 小学生




順列の問題 一定の条件で並べる 高校数学の知識庫



札幌から網走までの行き方は何通りですか 求め方 答え教えてくだ Yahoo 知恵袋




場合の数 大中小3つのサイコロを投げるとき何通り 奇数 偶数 4の倍数 数スタ




無料 中2数学 基本問題 問題プリント 235 確率3 意味 求め方1




無料 中2数学 基本問題 解答プリント 235 確率3 意味 求め方1




順列と組み合わせの公式とその違い 問題付き 理系ラボ
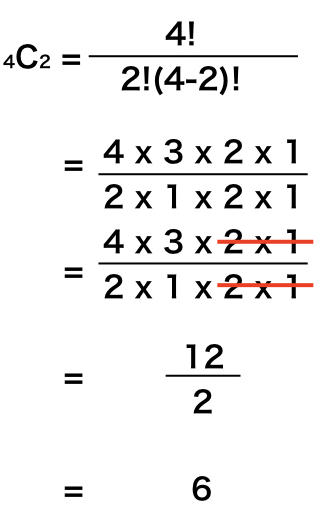



組み合わせ計算は何通り 重複も合わせる順列との違いを簡単攻略 Landgather



組み合わせ C とは 公式や計算方法 は何通り 受験辞典



組み合わせ C とは 公式や計算方法 は何通り 受験辞典



算数 数学 組み合わせの考え方 5人から2人を選ぶ なるほどの素




4桁の数字は何通りある 0 9や1 9の場合 6桁の数字は何通り パスワードやパスコードや暗証番号 ウルトラフリーダム




1 L 6 3 32 1 Left 1righ Descubre Como Resolverlo En Qanda




解き方解説 場合の数を計算で解く 場合の数は計算でサボれ




4人の中から2人選ぶ場合何通りの組み合わせがあるか 4人から3人選ぶ時は何通りか 5人から3人 4人を選ぶ場合何通りか 確率 More E Life




中学2年数学 確率 場合の数を求める問題の解き方 数学の面白いこと 役に立つことをまとめたサイト
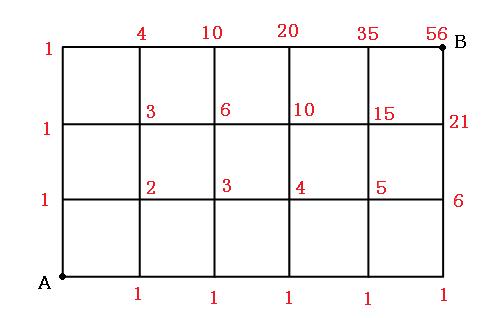



道順を求める場合の数の裏技 場合の数の道順は数字を書きこんでいけ
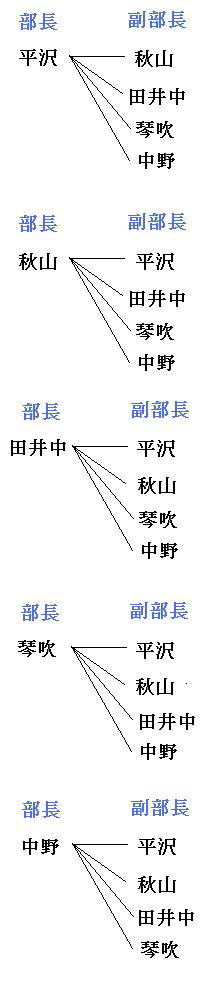



組合せと順列は何が違うのか 組合せは樹形図でも計算でも解ける



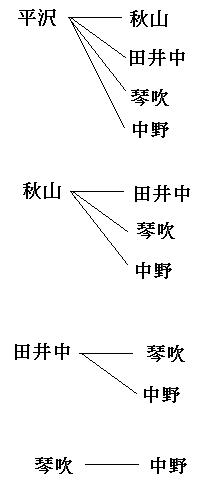
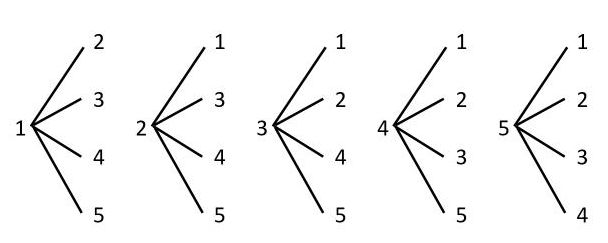
樹形図の書き方のコツと注意点 中学受験で 場合の数 をマスターする 中学受験ナビ




画像にある中央値の求め方の方法がわかりません Clear



1
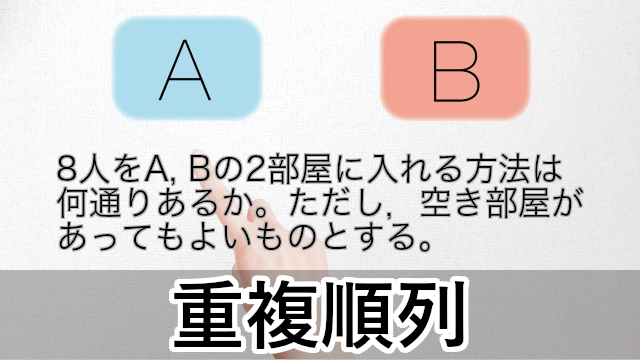



数学ia 重複順列の場合の数の求め方 大学入試数学の考え方と解法




順列と組み合わせの数の公式 どちらを使うのが正しいか迷ったときの便利なテクニック アタリマエ



Spi M54e217p7lcis9d Com Category E9 A0 86 E5 97 E7 B5 84 E5 90 81 9b




中学数学 場合の数



0 件のコメント:
コメントを投稿