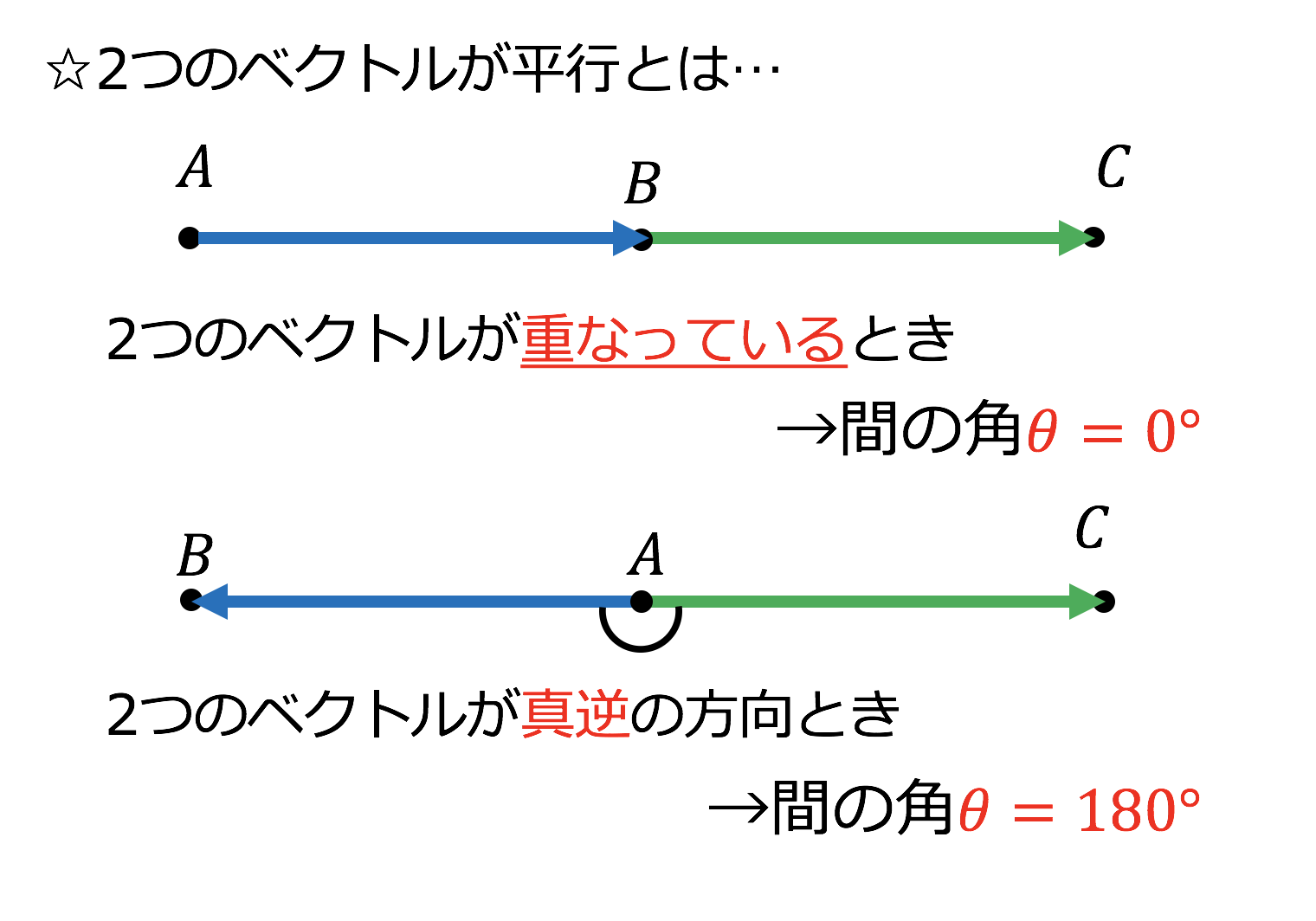
2つのベクトルが垂直のときの内積 ベクトルにおける垂直は超重要です。使用頻度がとても高いです。 平行のときと同じように考えていきます。 こちらも連想ゲームをやっていきま
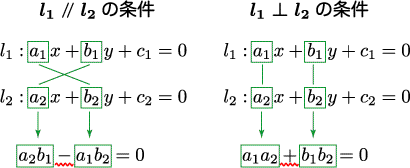
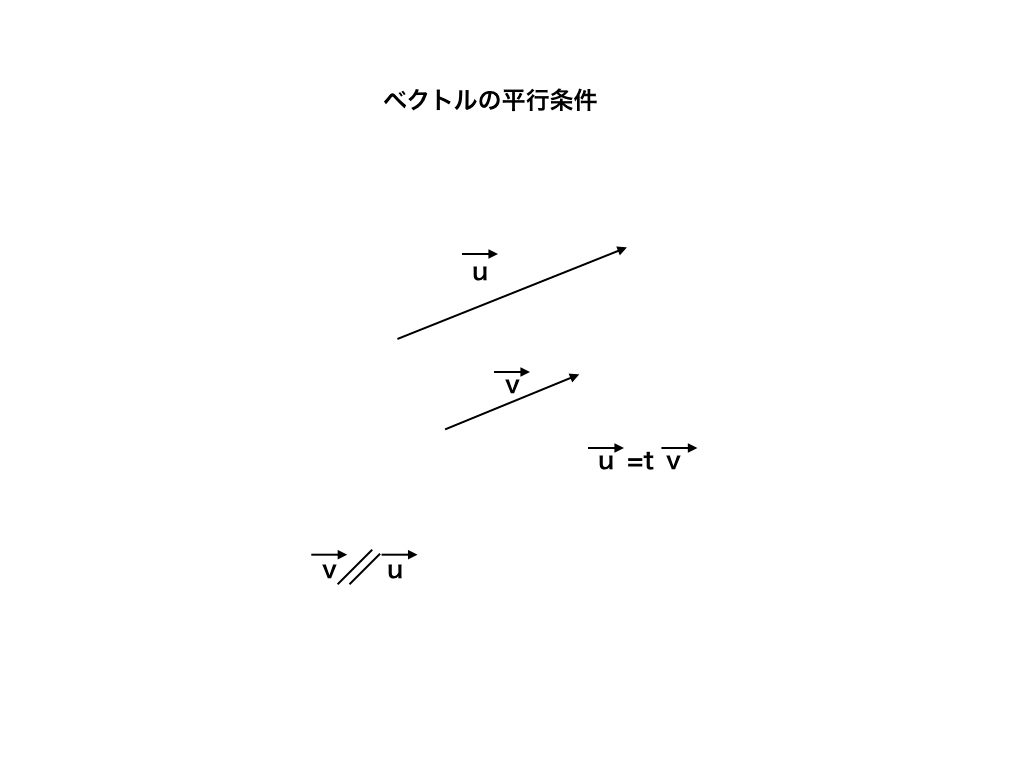
ベクトル 平行 垂直 分解- 平行四辺形 ABCD において,AD = 6,∠A = 1°, \overrightarrow {\text {AD}}=\vec {a} AD = a , \overrightarrow {\text {AB}}=\vec {b} AB= b ,AB = x x とする。 点 A から直線 CD ただし、どちらもゼロベクトルではないものとする。 つまり、 (x1,y1,z1) ≠ (0,0,0) かつ (x2,y2,z2)≠ (0,0,0) このとき、 垂直条件は内積が0になること。 つまり、x1y1x2y2z1z2=0
ベクトル 平行 垂直 分解のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  |  |
 |  |  |
 |  | |
「ベクトル 平行 垂直 分解」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
 |  |  |
「ベクトル 平行 垂直 分解」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
 |  | |
「ベクトル 平行 垂直 分解」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  | |
 |  |  |
「ベクトル 平行 垂直 分解」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 | ||
 |  |  |
 |  |  |
「ベクトル 平行 垂直 分解」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  | |
 |  |  |
「ベクトル 平行 垂直 分解」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「ベクトル 平行 垂直 分解」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
 | 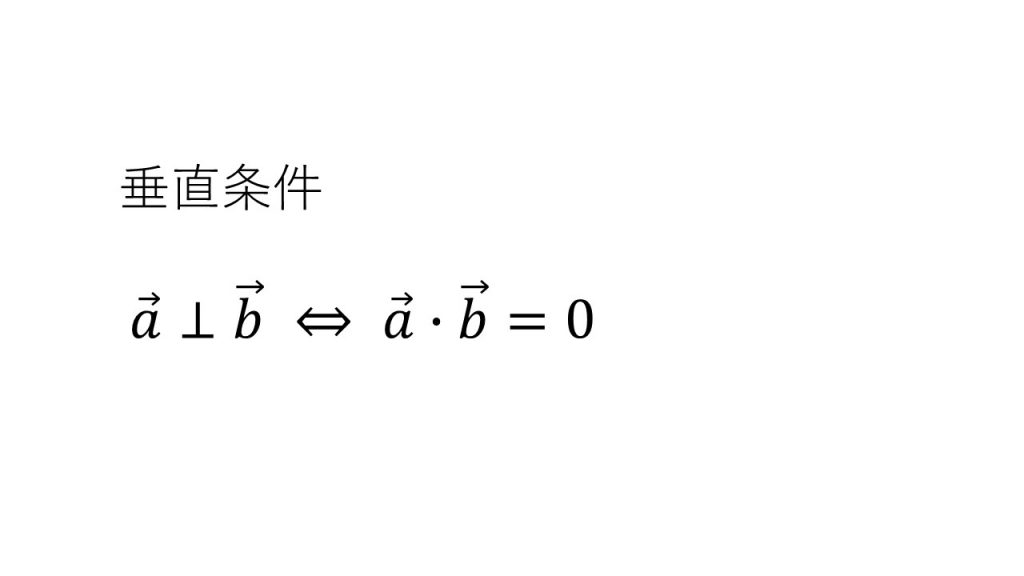 |  |
「ベクトル 平行 垂直 分解」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |
前回 https//googl/ghtH8T 次回 https//googl/IHSl5l動画のプリント(19ch) http//www19chtv/サブチャンネル とある男が結論からいうと、2つのベクトルについて、 内積が0 ならば 2つのベクトルは垂直である といえます。 上のポイントのうち①について解説します。 ベクトルの内積は、 (ベクトルaの大きさ)× (ベクト
Incoming Term: ベクトル 垂直 平行, ベクトル 平行 垂直 成分, ベクトル 平行 垂直 分解, 平行四辺形 ベクトル 垂直 証明, 平行四辺形 ベクトル 垂直,




0 件のコメント:
コメントを投稿